結構前に『「原因と結果」の経済学―――データから真実を見抜く思考法』という本を読みました。
因果関係という統計の中でも、数学の中でも難しい分野の入門書(興味がある人が一冊目に読む本)として非常にわかりやすかったです。
せっかく良い本を読んで、学ぶことが多かったので忘備録として本書の中で印象に残った部分と本書を読んだ感想をまとめようと思います。
以下、『「原因と結果」の経済学―――データから真実を見抜く思考法』から引用しています。気になる方はぜひ本書を読んでください
「因果と結果の経済学」とは?
タイトル:「原因と結果」の経済学―――データから真実を見抜く思考法
出版社 : ダイヤモンド社; 第1版 (2017/2/16)
中室牧子(なかむろ・まきこ)
慶應義塾大学 総合政策学部 准教授
慶應義塾大学環境情報学部卒業後、日本銀行、世界銀行、東北大学を経て現職。コロンビア大学公共政策大学院にてMPA(公共政策学修士号)、コロンビア大学で教育経済学のPh.D.取得。専門は教育経済学。著書にビジネス書大賞2016準大賞を受賞し、発行部数30万部を突破した『「学力」の経済学』(ディスカヴァー・トゥエンティワン)。
津川友介(つがわ・ゆうすけ)
ハーバード公衆衛生大学院 リサーチアソシエイト
東北大学医学部卒業後、聖路加国際病院、ベス・イスラエル・ディーコネス・メディカル・センター(ハーバード大学医学部付属病院)、世界銀行を経て現職。ハーバード公衆衛生大学院にてMPH(公衆衛生学修士号)、ハーバード大学で医療政策学のPh.D.取得。専門は医療政策学、医療経済学。ブログ「医療政策学×医療経済学」で医療に関するエビデンスを発信している。
著者の中室牧子(なかむろ・まきこ)さんは「学力」の経済学が有名ですね。
本書の目次
この本は目次が長く、丁寧なのが特徴的です。
目次
はじめに
メタボ健診を受けていれば長生きできるのかテレビを見せると子どもの学力は下がるのか偏差値の高い大学へ行けば収入は上がるのか「因果推論」を理解すれば思い込みから自由になれる
第1章 根拠のない通説にだまされないために
「因果推論」の根底にある考えかた「因果関係」「相関関係」とは何か因果関係を確認する3つのチェックポイント
1.「まったくの偶然」ではないか
2.「第3の変数」は存在していないか
3.「逆の因果関係」は存在していないか
因果関係を証明するのに必要な「反事実」タイムマシンがないと反事実は作れない?
反事実を「もっともらしい値」で穴埋めする「比較可能」なグループでないと穴埋めはできない反事実を正しく想像できないと根拠のない通説にだまされる?
COLUMN1 チョコレートの消費量が増えるとノーベル賞受賞者が増える?
第2章 メタボ健診を受けていれば長生きできるのか
因果推論の理想形「ランダム化比較試験」
「実験」を使えば因果関係を証明できる
なぜランダムに割り付けないとダメなのか
「メタボ健診」と「長生き」のあいだに因果関係はあるか
「統計的に有意」とは
健診を受けていても長生きにはつながらない
1200億円の税金が投じられたメタボ健診
「医療費の自己負担割合」と「健康」のあいだに因果関係はあるか
ランド医療保険実験の結果
自己負担割合を高くしても、貧困層以外の健康状態は変わらない
COLUMN2 複数の研究をまとめる「メタアナリシス」
第3章 男性医師は女性医師より優れているのか
たまたま起きた実験のような状況を利用する「自然実験」
手元にあるデータを用いて、実験のような状況を再現する
「医師の性別」と「患者の死亡率」のあいだに因果関係はあるか
女性医師が担当すると患者の死亡率が低くなる
「出生時体重」と「健康」のあいだに因果関係はあるか
出生時体重が重い赤ちゃんは健康状態がよい
COLUMN3 受動喫煙は心臓病のリスクを高めるのか
第4章 認可保育所を増やせば母親は就業するのか
「トレンド」を取り除く「差の差分析」
実験をまねる「擬似実験」
前後⽐較は意味がない
前後⽐較が使えない2つの理由
昨年の売上が「反事実」ならば前後⽐較は有効だが……
前後⽐較デザインを改良した「差の差分析」
差の差分析が成立するための2つの前提条件
「認可保育所の数」と「母親の就業」のあいだに因果関係はあるか
認可保育所を増やしても母親の就業率は上がらない
「最低賃金」と「雇用」のあいだに因果関係はあるか
最低賃⾦を上げても雇用は減らない
COLUMN4 「早く寝ないとお化けが出るよ」は正しい教育法か
第5章 テレビを見せると子どもの学力は下がるのか
第3の変数を利用する「操作変数法」
新聞の広告料割引キャンペーンを利用する
操作変数法が成⽴するための2つの前提条件
「テレビの視聴」と「学力」のあいだに因果関係はあるか
テレビを見ると偏差値が上がる
「母親の学歴」と「子どもの健康」のあいだに因果関係はあるか
母親が大卒だと生まれてくる子どもの健康状態がよい
COLUMN5 女性管理職を増やすと企業は成長するのか
第6章 勉強ができる友人と付き合うと学力は上がるのか
「ジャンプ」に注⽬する「回帰不連続デザイン」
「49人の店舗」と「50人の店舗」の違いを利用する
回帰不連続デザインが成⽴するための前提条件
「友人の学力」と「自分の学力」のあいだに因果関係はあるか
学力の高い友人に囲まれても自分の学力は上がらない
「高齢者の医療費の自己負担割合」と「死亡率」のあいだに因果関係はあるか
高齢者の医療費の自己負担割合が増えても死亡率は変わらない
COLUMN6 「ホルモン補充療法」の罠
第7章 偏差値の高い大学に行けば収入は上がるのか
似た者同⼠の組み合わせを作る「マッチング法」
似かよった店舗を探しだす
複数の共変量をひとまとめにする「プロペンシティ・スコア・マッチング」
プロペンシティ・スコア・マッチングが成立するための前提条件
「大学の偏差値」と「収入」のあいだに因果関係はあるか
偏差値の高い大学に行っても収入は上がらない
COLUMN7 ビジネス版ランダム化⽐較試験「A/Bテスト」
第8章 ありもののデータを分析しやすい「回帰分析」
因果関係の評価に適さないデータしかないときは……
データを表現する「最適な線」を引く
交絡因子の影響を取り除いてくれる「重回帰分析」
COLUMN8 因果推論はどのように発展してきたか
補論① 分析の「妥当性」と「限界」を知る
補論② 因果推論の5ステップ
おわりに
因果関係と相関関係は似ているけど違うもの
これ、日々の生活でよく間違えます。なんならデータを扱う専門家的な人もちょいちょい間違えます。かくいう自分も間違えることがあります。
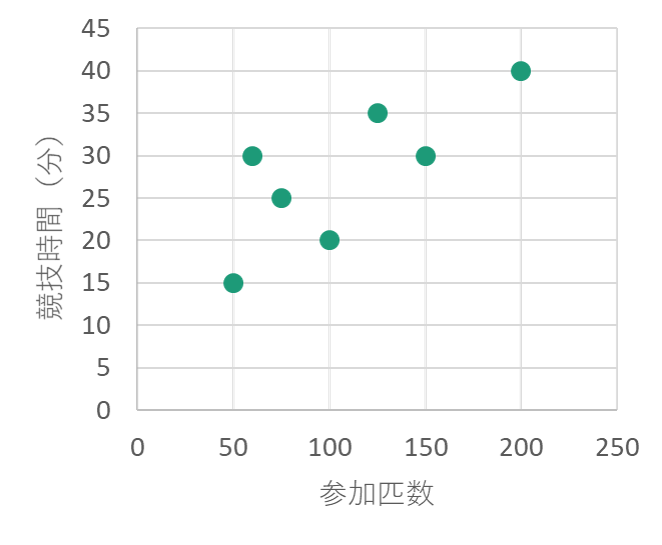
因果関係も相関関係もグラフにすると関係があるように見えます。
因果関係の場合はグラフで言うところの横軸が原因で縦軸に変化が起きています(または縦軸が原因で横軸に変化が起きている)。一方で、相関関係は横軸が原因で縦軸に変化が起きているように見えて、関係性は不明となっています。
2つのことがらのうち、片方が原因となって、もう片方が結果として生じた場合、この2つのあいだには「因果関係」があるという。一方、片方につられてもう片方も変化しているように見えるものの、原因と結果の関係にない場合は「相関関係」があるという(図表1-1)。相関関係の場合、何らかの関係が成り立っているものの、因果関係はない。
本書より一部抜粋
以下個人的な主観です。
なぜ、相関関係を因果関係とみてしまうのか?それは中学の数学からみている関数のグラフにあるのではないかと考えています。
y=f(x)
に代表されるこの表記では、横軸(x)の値が原因で縦軸yの値が生じるという関係を表しています。
グラフ
私たちは数学の勉強でこのy=f(x)のグラフをたくさん見て、勉強をしているはずです。これが相関関係を学ぶ時の混乱を起こしているのではないでしょうか?
相関関係でも以下のようにグラフで表されます。この時、無意識で横軸によって縦軸の結果が出ると考えてしまいます。
しかし、先ほども書いた通り、相関関係がわかっても因果関係は分かりません。つまり、縦軸と横軸は連動して動いているけれども原因はまだ不明という状態です。
高校で数学を学びすぎたことで逆に因果関係と相関関係の区別がつきにくくなっているのはないかと思い、ここまで書いてみました。
ちなみに、高校以降の数学でも逆関数などのように横→縦軸ではない見方をする考え方があります。これを学ぶ時も多くの高校生が苦戦していたと聞いたことがあります。(出典は忘れました。ごめんなさい)やはり、われわれはまじめに数学を勉強するほどに横軸→縦軸でグラフを見る癖が抜けないですね。お互い気を付けたいものです。
なぜ因果関係を知ることが重要なのか?
因果関係が存在しないことの何が問題なのか、と思う人もいるだろう。メタボ健診を受けないより受けたほうが、テレビばかり見るよりほどほどにしたほうが、偏差値の低い大学よりは高い大学に行くほうがましだろう、と考える人もいるのではないか。
私たちが何か行動を起こすときには、けっこうなお金や時間がかかる ことが多いということを忘れてはならない。因果関係があるように見えるが、実はそうではない通説を信じて行動してしまうと、期待したような効果が得られないだけではなく、お金や時間まで無駄にしてしまう。そのお金や時間をきちんと因果関係に基づいたことに用いれば、よい結果が得られる確率ははるかに高くなるだろう。
私たちは日々幸せになるため、成功するためなど様々な動機で行動をする。行動をするときには時間やお金、労力をかける。場合によっては人の力を借りることもある。つまり、タダではない何かしらをかけています。
タダではないものをかけるのであれば、きちんとリターンが欲しいですよね。
せっかく時間をかけてセミナーや講座を受けたのに学びが少ない。お金をかけて学習環境を整えたのに成績が上がらない。これでは悲しいですよね。
これが政策、教育、マーケティング、医療など人手とお金がかかる規模大きくなる、または国単位で影響が出ることであればなおさらですよね。「お金をかけて教育の政策をやったけど、効果がありませんでした」では私たち一般市民が納得するわけがありません。
物事の因果関係がわかれば、リターンを得やすいかどうかがわかりやすくなります。
もちろん、因果関係を示せたから100%リターンを得られるわけではありません、しかし、最初からリターンを得やすいということがわかるだけでも方針がたつことはこの世の中非常に多いのです。
因果関係がどうかを確かめる3つの視点
2つの変数の関係が因果関係なのか、相関関係なのかを確認するために、次の3つのことを疑ってかかることをおすすめしたい。その3つとは、 1.「まったくの偶然」ではないか 2.「第3の変数」は存在していないか 3.「逆の因果関係」は存在していないか である。
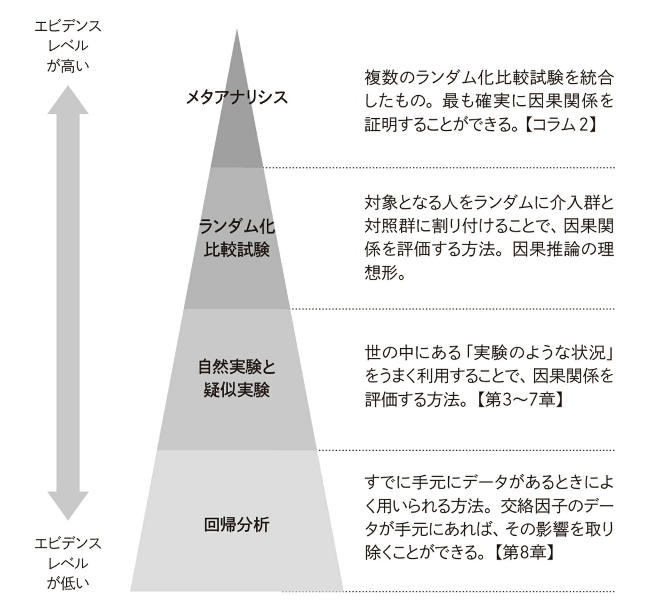
因果関係(エビデンス)の階層
因果関係のエビデンスにも序列があります。本を読めばわかるので、ここは図を引用して割愛。
因果関係を読み解く5つのステップ
ステップ1 「原因」は何か 原因と結果の「原因」である。広告と売上のケースであれば、「広告」にあたる。
ステップ2 「結果」は何か 原因と結果の「結果」である。広告と売上のケースであれば「売上」にあたる。
ステップ3 3つのチェックポイントを確認しよう 第1章で因果関係を確認するための3つのチェックポイント、(1)まったくの偶然ではないか、(2)交絡因子が存在しないか、(3)逆の因果関係は存在しないか、ということを疑ってかかる必要があるということはすでに述べた。
ステップ4 反事実を作り出そう 広告と売上のあいだに因果関係があるかどうかを確認するためには、あなたの企業が広告を出したときの売上と、仮に広告を出さなかったときの売上を比較する必要がある。この「仮に広告を出さなかったとき」が、まさに「反事実」である。
ステップ5 比較可能になるよう調整しよう 反事実をもっともらしい値で置き換える有力な方法は、「比較可能」なグループになるように調整する、ということである。
因果関係の推測はあまりにも奥が深い
この本の一文を抜粋しつつ、個人的になるほどと思った部分をまとめました。これからも因果関係に関する本は多く読むことになると思います。あまりにも奥が深いですし、学んだ分活かせることが多いので。