【小学3,4年生の算数】10倍した数と10で割った数（整数） | ×10と÷10の計算をマスターして大きい数の仕組みを理解しよう！

今回は小学校３，４年生で学ぶ内容です。整数で×10と÷10をした時を見てみましょう。日常生活で良く行う計算なのでマスターしましょう。

ポイント

大きな数字の掛け算の中でも「10倍」と「10分の1」はとても簡単なのに便利ですね。

せっかくなので例題を解きながら確認しましょう！

例題

ノートをもって実際に解いてから解答と解説を読んでくださいください。

解答と解説

×10は0を一つつける。÷10は0を一つ取り除く

でしたね。①で考えると50×10では50に0を一つつけてみましょう。500ですね。もう一つ50÷10では50の0を一つ取り除いてみましょう。50となります。できましたか？

下の図を見てください。答えを見ると、50×10をすると500になり、50からケタが一つ増えていますね。逆に50÷10をすると5になり、50からケタが一つ減っていますね。

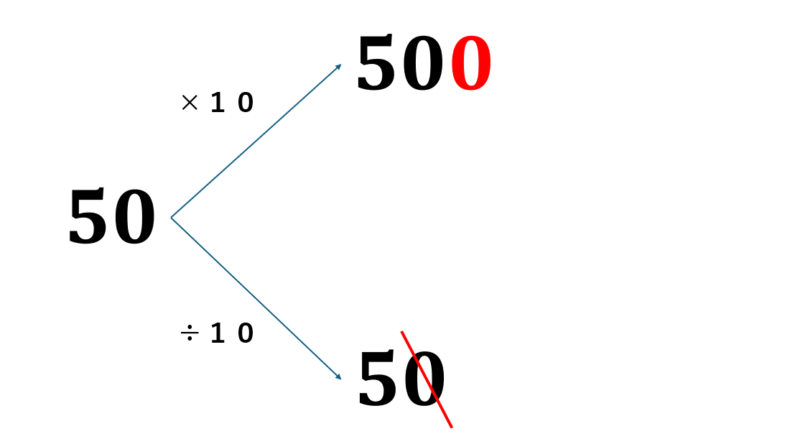
②と③も同じように解いてみてください。答え合わせです。

\begin{align*}
① \quad
&50 \times 10 = 500\\
&50 \div 10 = 5\\
② \quad
&120 \times 10 = 1200\\
&120 \div 10 = 12\\
③ \quad
&3500 \times 10 = 35000\\
&3500 \div 10 = 350\\
\end{align*}

イメージがつかめましたか？下に追加の問題を載せておきます。復習がてらにやってみてください。答えはこの記事の一番下に用意しています。

ちょっと難しい例題

補足でちょっと難しい例題をやってみましょう。これができると、この単元はマスターしたも同然です。こちらも紙とペンを持って解いてください。

こうやって書かれると分かりづらくなりますね。なぜわかりづらいかというと、数字なのに日本語で書かれているからです。

数字に直しましょう。１３万は130000ですね。

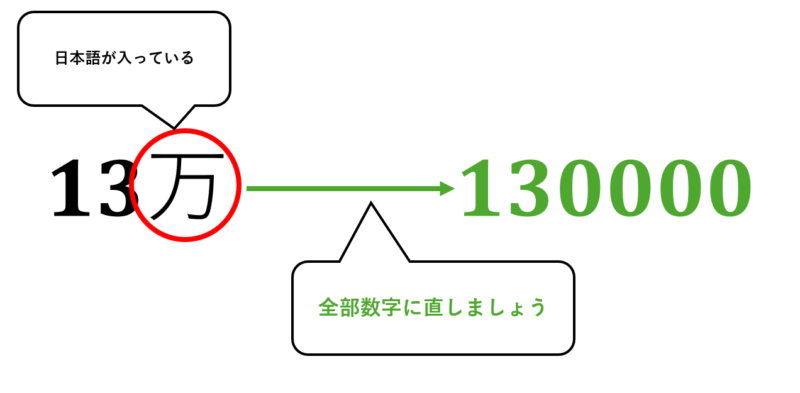
これならば、今までと同じようにできますね。

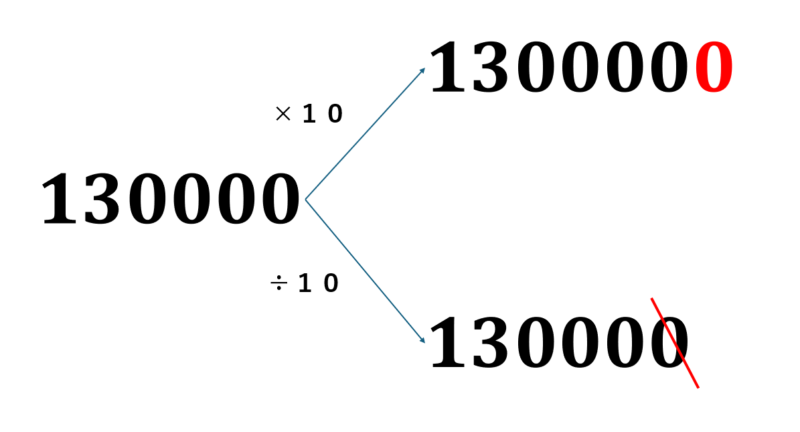
下に解答をのせておきます。

\(130000×10 = 1300000（130万と答えても正解です）\)

\(130000÷10 = 13000（1万3千と答えても正解です）\)

ここまでできると学校の授業で先生の言っていることが分からなくて困るということはなくなるのではないでしょうか？

最後に追加問題を用意しておきます。復習がてらにやってみてください解いてみてこの単元をマスターしてください。答えはこの記事の下に用意してあります。

今回のまとめ

今回は小学校３年生、４年生に向けて×10と÷10の計算をまとめました。ポイントは以下の通りです。文字にするとコンパクトですね。

×10では右に0を1つつける（1ケタ増える）
÷10では右の0を1つとる（1ケタ減る）

算数が苦手な人のためになるべく図を多くして丁寧に説明してみました。自分で手を動かしてやってみてください。難しければ保護者の人と一緒にやってみて下さい。

今回の話をさらに問題を解きながら理解を深めたい方は以下の本もおすすめです。

陰山メソッド 徹底反復 新版 算数プリント 小学校1～6年 （陰山英男の徹底反復シリーズ） [ 陰山 英男 ]

created by Rinker

• Amazon
• 楽天市場
• Yahooショッピング

追加問題の答え

補足説明（発展的内容） | ×10、÷10をケタ数と連動させてみる

小学5年生以上の説明を理解しやすくするために補足説明をします。発展的な内容なので、難しいと思った人は読み飛ばしてもらってもかまいません

今回は×10と÷10を以下のように計算するように説明しました。

今回の話までではこの方法でも解けるのですが、小学校５年生以降になると解けないケースが出てきます。具体的には数字のお尻の部分（一の位）が０でない数字や小数などです。

例えば３７を１０で割る時に０を取るといっても０はないですよね？

ということで、追加問題まで解いて今回の話を理解できた方のために、×10、÷10をケタ数と連動させて説明をします。そのためには×10と÷10の計算方法を以下のポイントで理解してもらいます。

先ほどからポイントの（）で書いている部分です。まず数字のケタについて確認します。

数字のケタ

数字にはケタがあります。日常生活でも◯ケタの数字という言い方をすると思います。

下の図のように一から始めて十、百、千・・・と右から順に読んでいきますね。千より大きな桁は万、億などと続いていきます。学校の授業などで下のような表を見たことがあると思います。

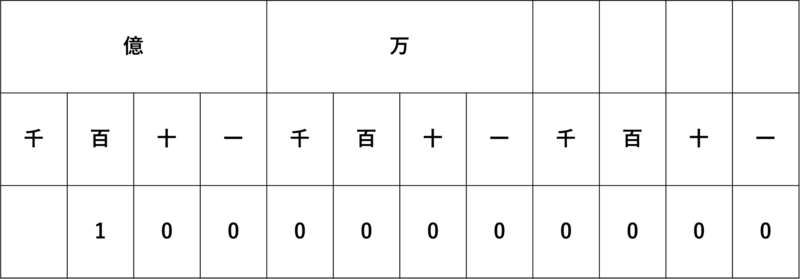
大きな数字のケタの読み方は別の記事でわかりやすく説明する予定ですので、そちらをご覧ください。

Coming Soon

×１０、÷１０とケタの操作を図で見てみる

で、これが×１０と÷１０にどのような関係があるのか？という話です。

例えば２３万という数字に×１０、÷１０をしてみましょう。今までの話と同様に２３００００として０をつけたり減らしたりすればいいですね。

これをケタの表に当てはめてみましょう。

×１０をすると数字が全体的に一つ左のケタへ移動しています。逆に÷１０をすると数字が全体的に一つ右のケタへ移動しています。この表から、

という言い方ができます。

ここまでの話を読んでもらうと

「話は分かるけど、なんでわざわざ違う言い方をするの？」

と思うかもしれません。この考え方は数字のお尻の部分（一の位）が０でない数字や小数などを×１０、÷１０するときに役に立ちます。というか、これをするためにわざわざこんな長ったらしい説明をしているのです。

お待たせしました。実際に一の位が０出ない数字を例にして×１０と÷１０をしてみましょう。

補足例題

小数を習った人はできると思います。改めてポイントを確認すると、

×10は数字を1ケタ増やす。または数字のケタを一つ左へスライドする

÷10は数字を1ケタ減らす。または数字のケタを一つ右へスライドする

でしたね。しつこいかもしれませんが、ポイントは何度確認してもいいですからね。

ケタの表に４７×１０と４７÷１０を行った結果をのせると以下のようになります。きちんと桁がスライドしていますね。

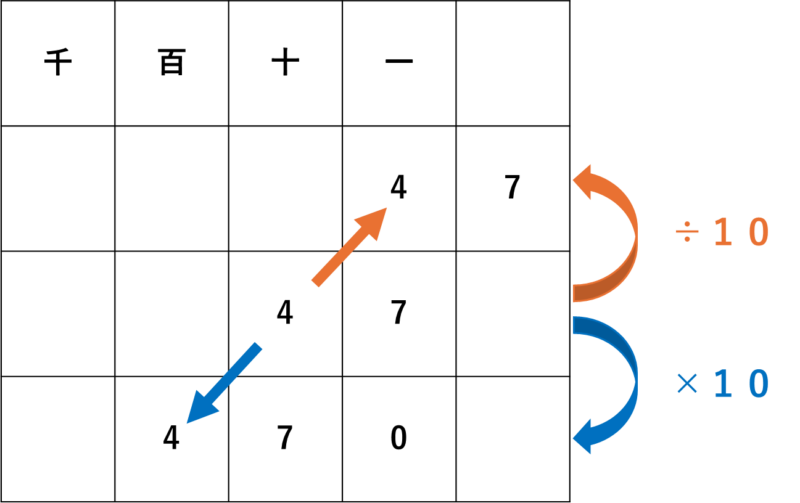
ここで問題なのは、４７÷１０をした時に１の位よりも左に数字があるということです。これが小学校の後半で習う小数になります。小数のケタの話もまた別の記事で詳しく説明すると思いますが、今のところは１の位の数字を÷１０すると小数第１位に移動すると理解してください。

ここまで説明すれば答えが出ますね。

\(４７×１０＝４７０\)

\(４７÷１０＝４.７\)

×10、÷10を小数点を絡める

小数点の説明を入れると×10、÷10の説明がさらにシンプルになります。

この説明であれば小学校５年生以降や中学生になっても問題なく計算ができます。小数も絡む数字での×10、÷10の計算はまた別の機会に練習しましょう。

Coming soon

さらにここまでの説明が理解できれば×100や×1000の計算も理解できる準備ができていますので、そちらも解説の記事を作りたいと思います。

Coming soon

もし、今すぐ練習したのであれば以下の本に練習問題が豊富にあるのでチェックしてみてください。