中学2年生になると数学が苦手になる人が中1よりも増えるのではないでしょうか。なぜならば、
多くの人が苦手とする単元が複数あり、しかもそれらが学期をまたいで登場し、つながりもよくわからない。
という事態になるからです。
中2数学の目次と苦手になりやすい単元
まずは目次を並べてみます。苦手になりやすい単元には☆印をつけておきます。
- 式の計算
- 式の計算、文字式の利用
- 連立方程式☆
- 連立方程式の解き方、連立方程式の利用
- 一次関数☆
- 一次関数とグラフ、一次関数と方程式、一次関数の利用
- 図形の調べ方
- 角と平行線の正式、三角形の合同条件
- 図形の性質と証明☆
- 証明問題について、三角形・四角形の定義と性質
- 場合の数と確率
- 場合の数とは確率とは、確率の求めかた
- データの活用
- 箱ひげ図、四分位数
学習のコツ
目次の順番通りに学習を進めると、「わけわからない文字や記述がたくさん出てきてよくわからないし、計算が多くて退屈」と感じるのではないでしょうか?この記事を読んでいるということは数学が苦手な人だと思うので。
そこで、中2数学を学習し始める前に、大きな目標を理解し、目標の部分を理解するために必要な内容を確認しましょう。
中2数学では大きな3つの目標があります。
1.1次関数を理解する
2.図形の証明をできるようにする
3.確率を計算できるようにする
1.1次関数を理解する
中1で学習した反比例は出てきません。その代わり直線のグラフ(1次関数といいます)が動いたり、ぶつかったりします。
動く関数
中2の数学では比例のグラフの角度や初期位置が変わります。
「こんなの現実で使うの?」と思う人もいると思うので、グラフを2Dのゲームと考えると分かりやすいと思います。

画面上のキャラをジャンプさせてみるとこんな感じで動きます。この直線的な動きを関数とみると分かりやすいかもしれません。

そして、ゲーム画面としてみるとキャラクターによって、そして場面によって動き方を変えたいですよね。キャラ移動の角度と初期位置を変えると動きに変化をつけれそうです。

*以上、正確な話ではありませんが、イメージをしてもらうための説明でした。ゲームで使う数学と物理の正確な話に興味を持った方は以下のような本を読んでください。難しいですが、ゲームの裏側が理解できておもろいですよ
*画像参照ゲーム
グラフを動かしたい
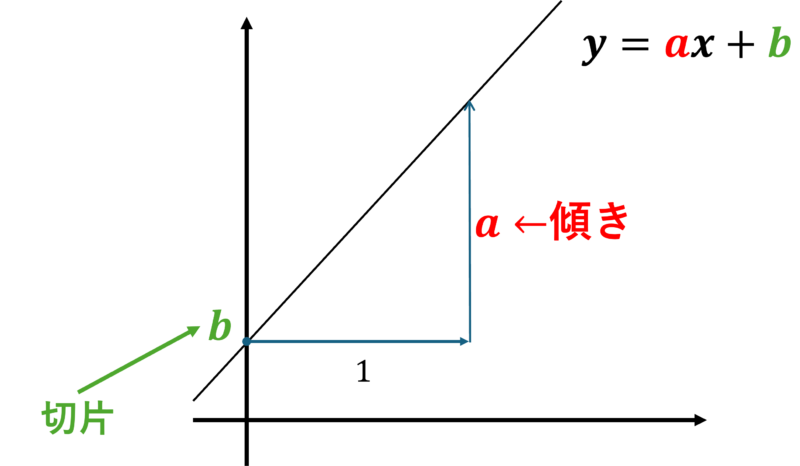
グラフに話を戻すと、グラフの角度と位置を変化させることでグラフを動かしたい。これが中2でやる1次関数のメインの話です。y=axのaを変化させることでグラフの角度が変わりますね(これを傾きといいます)。また、変化の割合という話が出てきますが、中2時点では「傾き=変化の割合」です。
そしてy=ax+bとしてbを加えるとグラフの初期位置が変化します。この初期位置であるbを切片といいます。
ぶつかる1次関数
次に1次関数で重要な2つ目の考え方であるぶつかる1次関数について少し話をします。
関数というものをゲームのキャラクターなどの軌道に例えても、スポーツにおけるボールの軌道に例えたとしても、関数が1つだけで完結することは少ないですよね。
ふたたびゲームで例えるとするならばゲームではたいていキャラクターが2体以上います。そして、何かしらの形でキャラクター(FPSや対戦ゲームで言えばキャラと弾が)がぶつかることがあるでしょう。


ということで、関数において2つ以上の関数がぶつかるということが重要である場面があり、式で表現したいわけです。
1次関数で2つの直線がぶつかる点を計算するためには関数を表す2つの式(これを方程式といいましたねy=axみたいなやつです)を解く必要があります。これを連立方程式といいます。
中2でいきなり連立方程式とかいう訳のわからない名前で2つの方程式を解かなければいけない理由が分かりましたね。
そして、連立方程式を解くためには中1でやった文字式と方程式のルールに加えて、方程式を解くためのルールを知る必要があります。そのため、最初に式の計算をやらなければいけません。
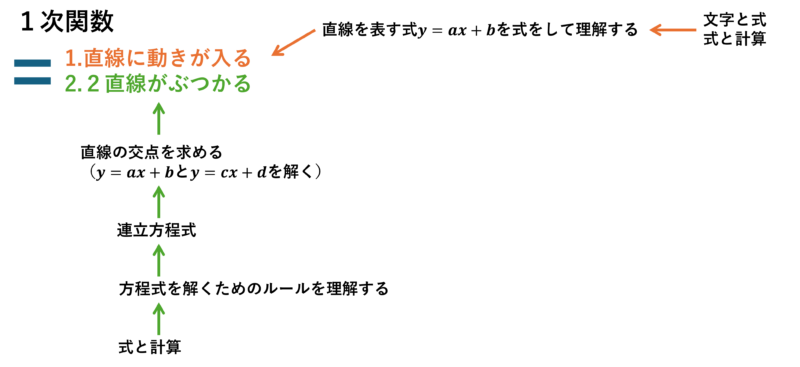
この順番が分からないので勉強がしづらいのと、連立方程式でも式と計算でも1次関数で使う計算以外の物(2次式など)も少し入るのでややこしいですね。
加えて、連立方程式は1学期、1次関数は2学期に入ってからやる学校の場合さらに分かりづらくなります。
学習は大変ですが、つながりが分かると難しさは軽減されると思います。何なら1次関数から逆の順番で学習しても良いのではないかと思ったりもします
2.図形の証明をできるようにする
図形のルールを利用して、新たなルールを見つけるということを行います。実は数学ではルールを使って問題を解くだけでなく、ルールを使って新しいルールを見つけるということをよく行います。
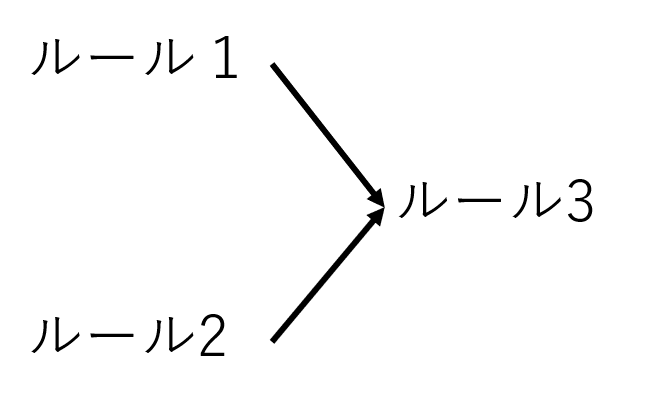
今まではルールを使って問題を解けばよかったのですが、「図形の証明」のタイミングでいきなり「ルールを使って新しいルールを見つける」という作業を行います。この単元、何が大変かというと
・「ルールを使って新しいルールを見つける」といういままでやったことのない行為を前触れなしで(何なら永遠にちゃんとした説明をされることなく)やらなければいけない
・今までのように答えだけを書くのではなく、答えまでのプロセスを書かされる
・数学特有の「結論を想像してから、手順を説明する」という技術を前触れなしで要求される(これまた永遠に説明されないこともある)
という一つだけでも大変なことを3つもやらされるのです。しかも、この3つの難しいことが、実は図形に限らない数学という科目で一般的に用いる話なのです。
つまり、初学者にとっては図形の公式を覚えて使えるようにするだけで大変なのに、図形の学習と関係ない話を図形の公式よりも多い分量でねじ込まれる羽目に合うのです。しかも、前触れや説明がされないまま。
ということで、この単元は2つに分けて学習をしましょう
①図形にまつわる基本的なルールを知る
②証明問題をするために必要な記述方法と思考方法を理解する
このブログでは主に①の説明をしますが、要望があれば②も解説します。
3.確率を計算できるようにする
これは目次のとおり、確率を学習してください。くじ引きやサイコロの話がメインになると思います。ポケモンが好きな人は雑に命中率の話だと思ってもらえれば結構です

中1で学習した資料の活用と確率、そして中3で学習する標本調査等が合わさって「統計」というわけのわからない代物が生まれるとぼんやり思っていてください。
もし詳しい説明が欲しいという要望があれば動画や記事にします
中2数学を学習するためのおすすめの教材
最後に中2数学を攻略するためにおすすめの本をいくつか紹介します(できれば自分のブログなどを見てほしいですが)。
教科書ガイド
教科書を読んで問題なく理解できるのであれば教科書を使い、教科書ガイドを補足資料として使えばよいと思います。
中2数学をひとつひとつわかりやすく。改訂版 (中学ひとつひとつわかりやすく)
数学の参考書の中でいちばんやさしい教材はこれになるのでしょう。そもそも教材を読めれば苦労はしないかもしれませんが、読んでいて「これならいけそう!」と思ったら使ってみてください。
最後に
結局は目次の最初から順番に学習するのですが、何をするために今の単元をやっているのかが分かれば、学習がしやすくなるはずです。
それぞれの単元の解説は別の記事で行う予定ですのでリンクから飛んで読んでくれると嬉しいです。