割り算の基本概念
割り算は、ある数をいくつかのグループに均等に分ける操作です。例えば、6個のあめを3人に均等に分けると、1人あたり2個のあめがもらえます。これを数式で表すと、6 ÷ 3 = 2 となります。
割り算の意味
6 ÷ 3 = 2 であれば、
「6を3個に分けたら1個のかたまりはいくつになるでしょうか?」
というのが割り算の意味です
ポイント
割り算は掛け算の逆を使う!
これは、割り算の問題を解くときに掛け算の知識を使って確認できるという意味です。例えば、6 ÷ 3 = 2 が正しいかどうかを確認するために、3 × 2 = 6 と掛け算してみます。この結果が元の数と一致することを確認します。
例題: 6 ÷ 3 = 2
- 「6個のあめを3人に分ける」と考えます。
- 割られる数(6)を、割る数(3)で割ります。
- 6 ÷ 3 = 2となります
- 掛け算で確認をします
- 3 × 2 = 6
今までの話を下の図にまとめておきました。
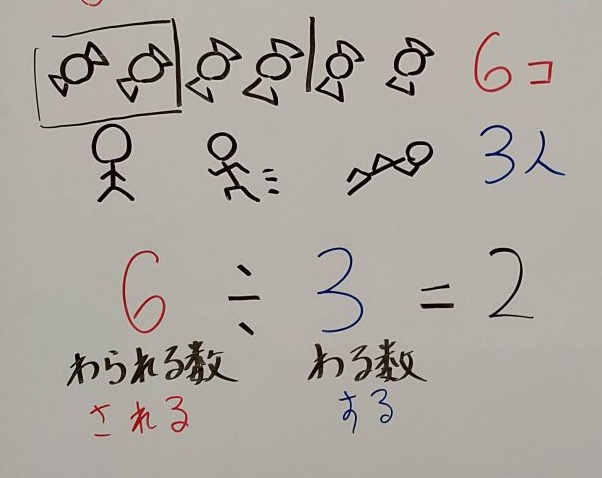
割り算の具体的な方法
割り算は掛け算の逆を使う!
でしたね。実際、6÷3=2を見てみると、割る数(3)と答え(2)をかけると割られる数(6)になります。ということは6÷3であれば、
3に何をかけたら6になるだろう?(3×○=6の○)
と考えればよいというわけです。1つ割り算を考えてみましょう。
例題: 32÷8を考える
先ほどの話であれば、
8に何をかければ32になるか?(8×○=32の○)
を考えればよいというわけです。8の段の九九ができれば答えは4だとわかるでしょう。(8×4=32)
下の図で対応関係を確認してください。
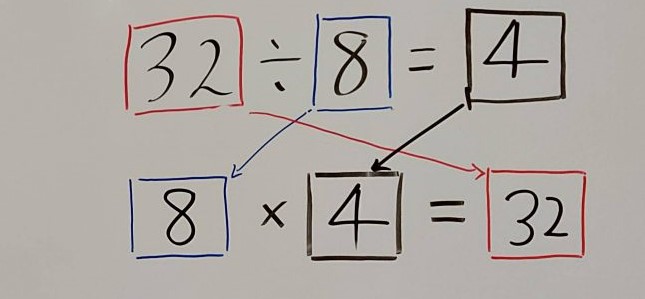
練習問題とその解説
練習問題で今回の話が理解できたかを確認してみましょう。練習問題で今回の話が理解できたかを確認してみましょう。
練習問題
- 12 ÷ 3
- 36 ÷ 6
- 21 ÷ 7
- 42 ÷ 6
- 35 ÷ 5
- 72 ÷ 9
- 56 ÷ 7
確認
- 12 ÷ 3 = 4
- 3 × 4 = 12
- 36 ÷ 6 = 6
- 6 × 6 = 36
- 21 ÷ 7 = 3
- 7 × 3 = 21
- 42 ÷ 6 = 7
- 6 × 7 = 42
- 35 ÷ 5 = 7
- 5 × 7 = 35
- 72 ÷ 9 = 8
- 9 × 8 = 72
- 56 ÷ 7 = 8
- 7 × 8 = 56
練習を続けましょう!
簡単な割り算は九九ができればかなり楽に解けます。練習を通じてマスターしましょう。




