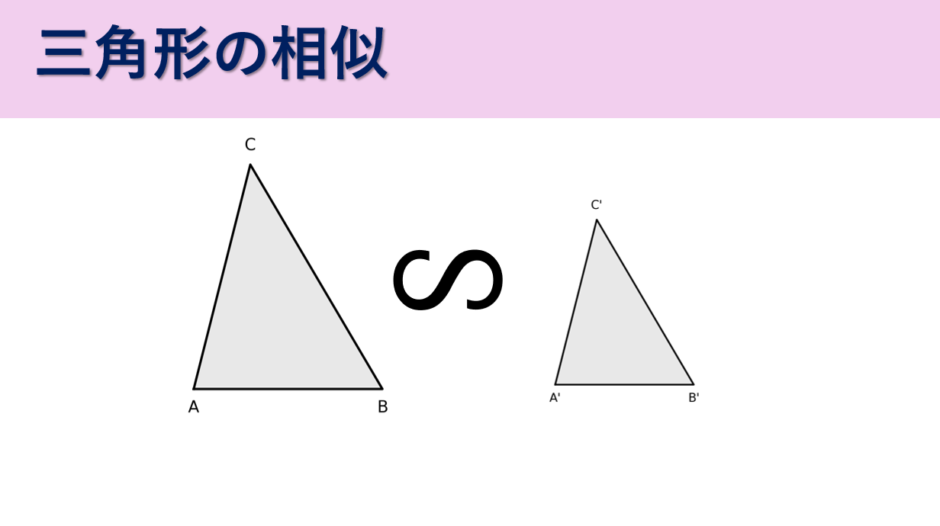
三角形が相似であるとは、形は同じで大きさが異なる図形であり、形を保ったまま拡大・縮小の関係にあることを示します。
三角形が相似であるか判断するための3つの条件をまとめました。復習や確認のご利用ください
目次 非表示
ポイント
三角形が相似である条件は以下の3つです(いずれか1つが成り立てば相似といえる)。
- 2つの角がそれぞれ等しい(2角相等)
- 3辺の比がすべて等しい(3辺比相等)
- 2辺の比が等しく、その間の角が等しい(2辺比相等と1角相等)
①2つの角がそれぞれ等しい(2角相等)
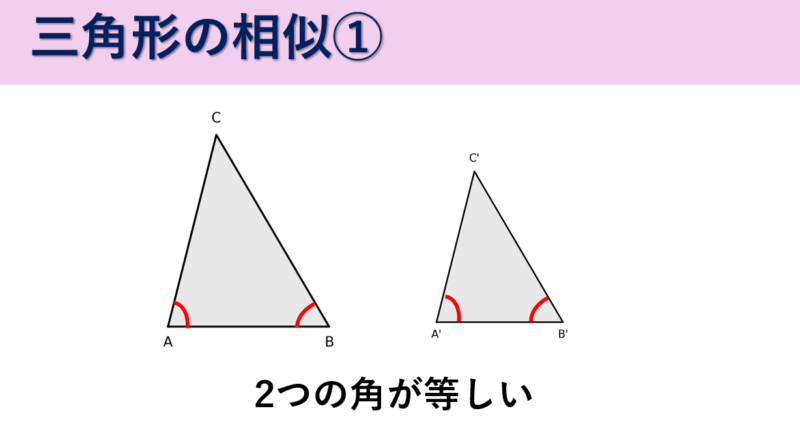
三角形の2つの角がそれぞれ等しい場合、もう1つの角も等しくなるため相似です。
②3辺の比がすべて等しい(3辺比相等)
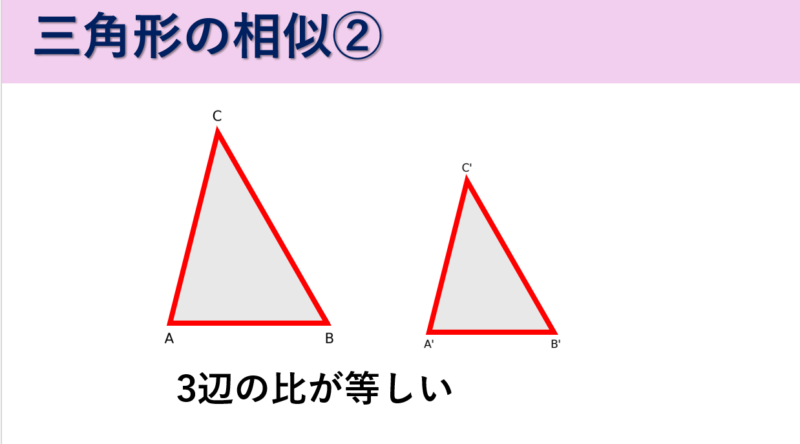
2つの三角形の3辺の長さの比がすべて等しい場合、相似です。
③2辺の比が等しく、その間の角が等しい(2辺比相等と1角相等)
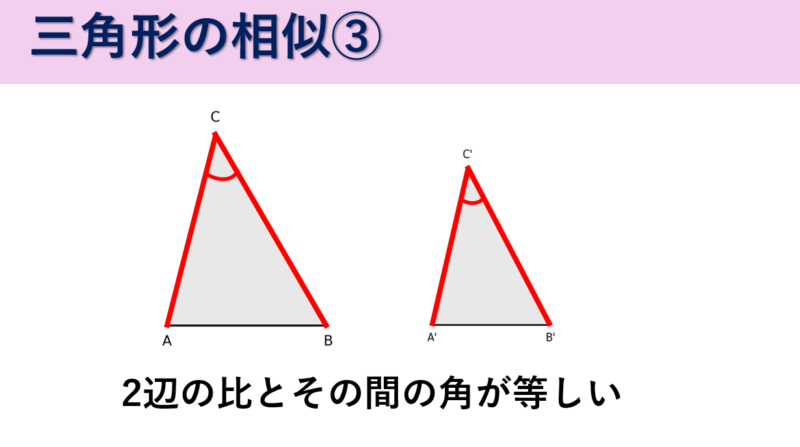
2つの三角形で、2辺の比が等しく、その間の角が等しい場合、相似です。
相似とは何か
相似とは、形は同じで大きさが異なる図形の関係を指します。一方の図形を拡大または縮小することで、もう一方の図形と重ね合わせることができる場合、これらの図形は相似であるといいます。相似な図形では、対応する角の大きさは等しく、対応する辺の長さの比は一定です。
覚え方
ChatGPTに覚え方を聞いてみたらこんな回答が出ました。
「2角・3辺・2辺1角!」
2角が等しい、3辺の比が等しい、2辺とその間の角が等しい、という順序で覚えましょう。キーワードで「にさんにいち(2角、3辺、2辺1角)」と覚えるのもおすすめです。
ごろや歌いながらサクッと覚えて、簡単な問題を解いてみると良いでしょう
公式、定理、ポイントの使いどころ、目印
図形の縮図や拡大図を扱う場合
例えば、地図の縮尺や模型の設計図などで応用されます。
与えられた辺や角を使って相似を証明したい場合
- 問題文に「平行」「等しい角」「辺の比」などのキーワードがあれば、相似の条件をチェックします。
例題
問題
次の三角形が相似であることを証明しなさい。
三角形 ABC の辺の長さ: AB = 6, BC = 8, CA = 10
三角形 DEF の辺の長さ: DE = 3, EF = 4, FD = 5
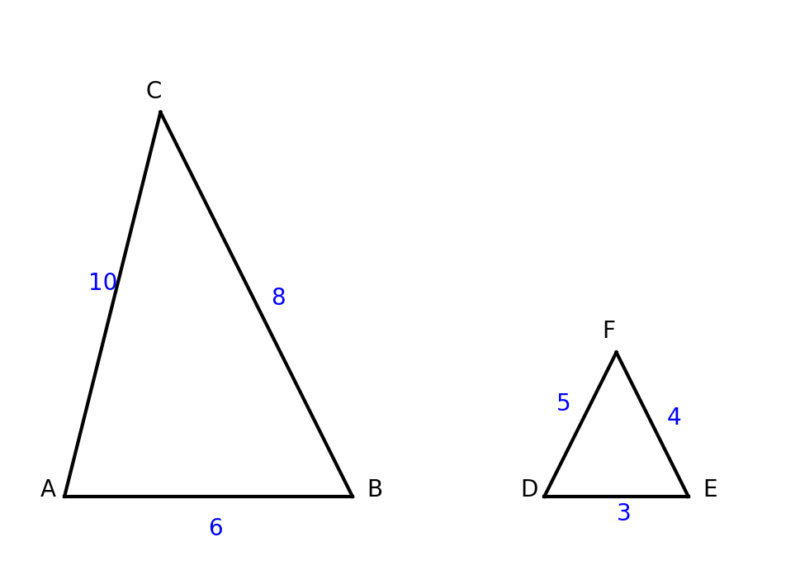
2つの三角形が相似であることを証明せよ
解答と解説
解答
- 三角形の3辺の長さを比べます。
$$ \frac{AB}{DE} = \frac{6}{3} = 2, \quad \frac{BC}{EF} = \frac{8}{4} = 2, \quad \frac{CA}{FD} = \frac{10}{5} = 2 $$ - 3辺の比がすべて等しいので、「3辺比相等」の条件より
$$ \triangle ABC \sim \triangle DEF $$
解説
- 3辺の比をそれぞれ確認することで3辺比相等の条件が満たされていることが分かります。
- 比の計算を確実に行うために、分母と分子をチェックしましょう。
まとめ
今回は三角形の相似の条件をまとめました。三角形の相似条件は「2角相等」「3辺比相等」「2辺比相等と1角相等」の3つです。問題を解きながら条件を理解しましょう。
相似を考える時には比や角度に注目して条件を満たしているか確認します。このタイミングで比の計算を復習しておくと掃除の理解が深まると思います。