連立方程式の解きかたには
①加減法
②代入法
の2つがあります。教科書などでは①の加減法から説明をしていきます。しかし、個人的には代入法が楽だと考えています。代入するだけでよいのでミスも少ないです。
まず代入法を考える。面倒であれば加減法をやってみる
ということで、この記事も代入法から説明します。例題は以下の式でやってみましょう
\begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=5…①\\
-x+y=-3…②
\end{array}
\right.
\end{eqnarray}
代入法
代入法とは一方の式にもう片方の式を代入して求める方法です。手順は以下の通り
(1)一方の式をx=またはy=の形にする
(2)もう一方の式にx=またはy=の形にした式を代入する→xまたはyが求まる
(3)求まったxまたはyを代入して解が算出される
こうやってまとめるとわかりづらいかもしれませんが、解いてみると案外簡単ですよ。実際に例題を解いてみましょう。
\begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=5…①\\
-x+y=-3…②
\end{array}
\right.
\end{eqnarray}
まずは自力で代入法をやってみましょう。解き終わったら下の解説を読んでください。
(1)一方の式をx=またはy=の形にする
①と②の式を眺めてどちらがx=またはy=にできるか考えます。今回は②の方が簡単にできそうですね。②の式を変形させましょう。
\( -x+y=-3…② \)
y=にした方が簡単にできそうですね。xを移項するだけなので
\( -x+y=-3 \Longleftrightarrow y=x-3 \)
(2)もう一方の式にx=またはy=の形にした式を代入する→xまたはyが求まる
変形した式を①に代入しましょう。\( 2x-3y=5…①\)
$$ \begin{align*} 2x-3y=5 & \Longleftrightarrow 2x-3(x-3 )=5 \\ & \Longleftrightarrow 2x-3x+9 =5 \\ & \Longleftrightarrow -x+9 =5 \end{align*} $$
ここまで来たらxは求まりますね。
$$ \begin{align*} -x=-4 \Rightarrow x=4 \end{align*} $$
(3)求まったxまたはyを代入して解が算出される
このxを②に代入します。\( y=x-3…① \)
\( y=4-3=1 \)
これですべての解が求まりましたね。
\begin{eqnarray}
\left\{
\begin{array}{l}
x=4\\
y=1
\end{array}
\right.
\end{eqnarray}
別解
先ほどの解説ではy=の形にしました。ここではあえてx=の形で解いた場合も載せておきますね。
$$ -x+y=-3…② $$
これをx=の形にすると、移項して両辺にマイナスをかけて、
$$ x=y+3 …②’$$
となります。これを①に代入して、
$$ \begin{align*} 2x-3y=5 & \Longleftrightarrow 2(y+3)-3y=5 \\ & \Longleftrightarrow -y+6=5 \\ & \Longleftrightarrow y=1 \end{align*} $$
このyを②’に代入して、
$$ x=1+3=4 $$
同じように解けましたね。
\begin{eqnarray}
\left\{
\begin{array}{l}
x=4\\
y=1
\end{array}
\right.
\end{eqnarray}
加減法
加減法とは式同士を足し算、引き算をして文字を消すことによって方程式を解く方法です。こちらも手順を書いておきます。
(1)問題の式を見て消す文字を決める
(2)消す文字の係数に合わせて式を掛け算する
(3)式全体を足し算または引き算をする→xまたはyが求まる
(4)求まったxまたはyを代入して解が算出される
では早速例題を使って説明します。例題はさっきと同じものを使いましょう。その方がわかりやすいと思うので。まずは加減法で解いてから下の説明を読んでください。
\begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=5…①\\
-x+y=-3…②
\end{array}
\right.
\end{eqnarray}
(1)問題の式を見て消す文字を決める
どちらの文字を消すかを決めます。今回はどちらで消しても難しさは変わらないと思います。ここでは\( x \)を消すようにしましょうか。
(2)消す文字の係数に合わせて式を掛け算する
\( x \)を消すためには②を2倍すれば(①式全体+②式全体)とできそうです。
ということで、②全体を2倍しましょう
$$ ② \times 2 \Longleftrightarrow 2(-x+y)=2(-3) \\ \Longleftrightarrow -2x+2y=-6 …②’ $$
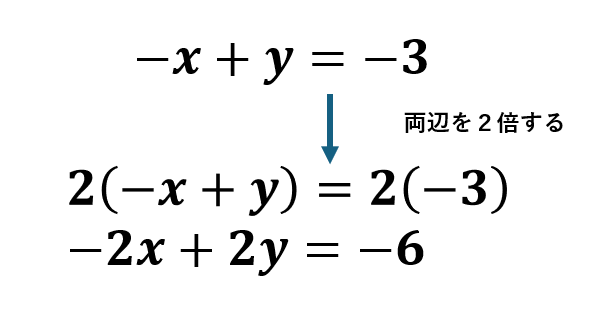
(3)式全体を足し算または引き算をする→xまたはyが求まる
①と②’を足しましょう。
$$ ①+②’ \Longleftrightarrow -y=-1 \\ \Longleftrightarrow y=1 $$
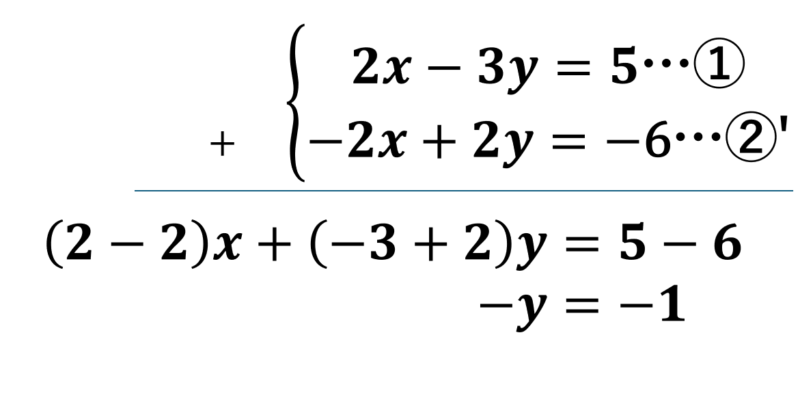
(4)求まったxまたはyを代入して解が算出される
y=1を①または②に代入します。計算しやすいほうに入れてください。
①に代入した場合
\( 2x-3=5 \Longleftrightarrow 2x=8 \Longleftrightarrow x=4 \)
②に代入した場合
\( -x+y=-3\Longleftrightarrow -x+1=-4 \Longleftrightarrow x=4 \)
どちらも同じ解になりますね。
\begin{eqnarray}
\left\{
\begin{array}{l}
x=4\\
y=1
\end{array}
\right.
\end{eqnarray}
別解
先ほどは\( x \)を消して解いたので、ここでは\( y \)を消した場合を説明しておきます。
この場合、②を3倍します。
$$ ② \times 3 \Longleftrightarrow 3(-x+y)=3(-3) \\ \Longleftrightarrow -3x+3y=-9 …②” $$
①と②”を足すとxが求まります。
$$ ①+②” \Longleftrightarrow -x=-4 \\ \Longleftrightarrow x=4 $$
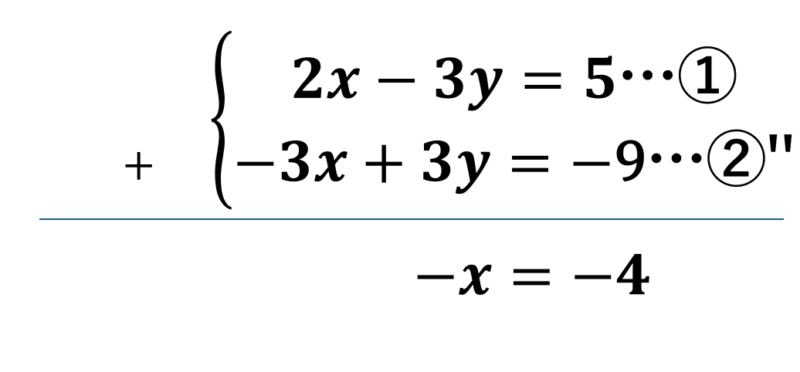
このxを①または②に代入すると解けます。
①に代入した場合
\( 2x-3y=5 \Longleftrightarrow 8-3y=5 \Longleftrightarrow y=1 \)
②に代入した場合
\( -x+y=-3\Longleftrightarrow -4+y=-3 \Longleftrightarrow y=1 \)
\begin{eqnarray}
\left\{
\begin{array}{l}
x=4\\
y=1
\end{array}
\right.
\end{eqnarray}
最後に
今回は連立方程式の解きかたを一つの例題で解説しました。どの方法を使っても求まることがわかったと思います。その時に自分が解きやすいと思った方法で解いてください。
この記事を読みながらテスト勉強や予習をしてください。手元にある問題集で解けばやり方がわかると思います。
もし、手元の問題集がしっくりこなかったら市販の問題集もあるので気に入ったものを使ってください。分量が少なくて、解説が肌に合うものがいいですね。