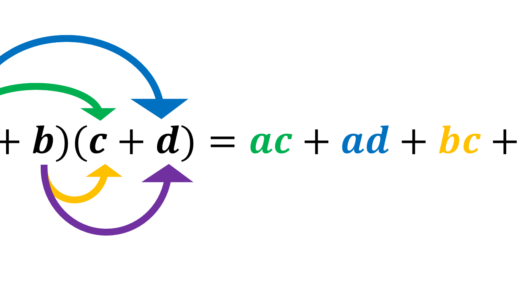因数分解のやり方は大きく分けて3つあります
①共通部分をくくる
②公式を使う
③大きな塊を見つける
①共通部分をくくる
一番シンプルで一番奥が深いのが「くくる因数分解」です。高校生になっても付き合うことになる考え方です。問題を解く中で勘どころを身に付けたいところです
共通の文字と数字を探してくくります。
\( 2ab+7ax \)を因数分解します。
aがどちらの項にも含まれているので、aをくくります。
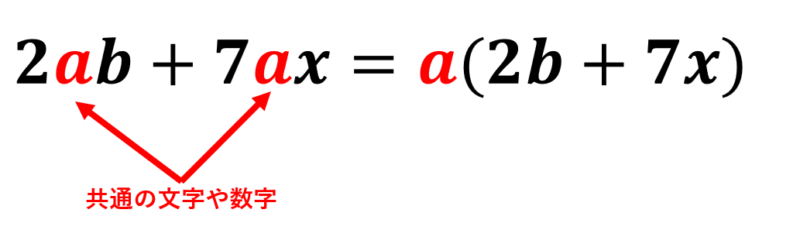
続いて、\( 8xy^2+12x^2y \)を因数分解してみましょう。こちらの共通の数字や文字を見つけると、どちらの項にも4xyがあることがわかります。
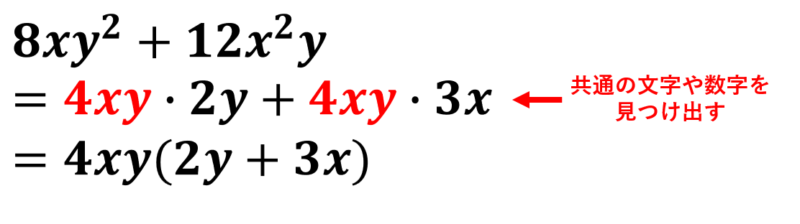
②因数分解の公式
因数分解の公式を覚えて、公式を使って因数分解を行います。まずは公式を一気に見ていきます。
\(
1.x^2+(a+b)x+ab = (x+a)(x+b) \\
2.x^2+2ax+a^2 = (x+a)^2 \\
3.x^2-2ax+a^2 = (x-a)^2 \\
4.x^2-a^2 = (x+a)(x-a) \\
5.acx^2+(ad+bc)x+bd = (ax+b)(cx+d)\\
\)
5.は応用的な内容ですので、まずは1~4を頭に叩き込みましょう。これらの式は展開公式(乗法公式)の逆になっていることもここで確認してください。展開公式(乗法公式)を忘れたという人は以下のリンクから確認してください。
\( 1.x^2+(a+b)x+ab = (x+a)(x+b) \)
足して\( a+b \)、かけて\( a \times b \)になる数の組み合わせを探す
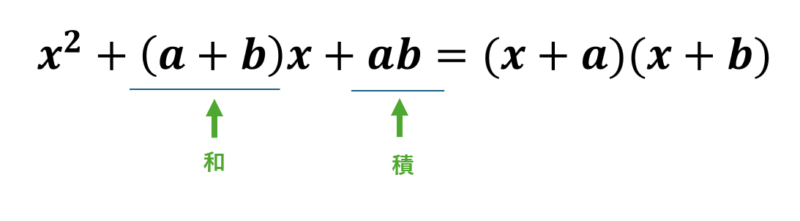
今ひとつピンと来ないかもしれませんが、とにかく数を探すということです。例題を一つやってみましょう
\( x^2+3x+2 \)
この場合は「足して+3、かけて+2」になる数を探します。今回だと+1と+2が見つかります。
\( (+1) + (+2) = +3 \)
\( (+1) \times (+2) = +2 \)
これを公式に当てはめると出来上がりです。
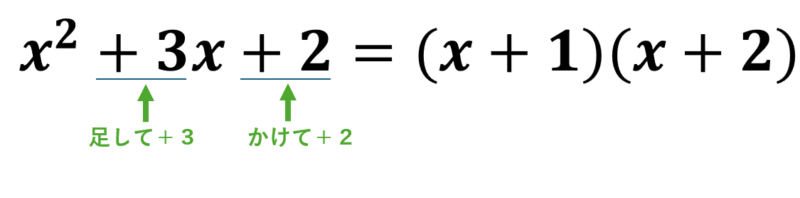
\( 2.x^2+2ax+a^2 = (x+a)^2 \)
先ほどの、\( x^2+(a+b)x+ab = (x+a)(x+b) \)でa=bとしてみると、この公式ができます。

例えば、\( x^2+8x+16 \)を解いてみましょう。
4の2倍が8、4の2乗が16であることに気が付けば解けます。

\( 3.x^2-2ax+a^2 = (x-a)^2 \)
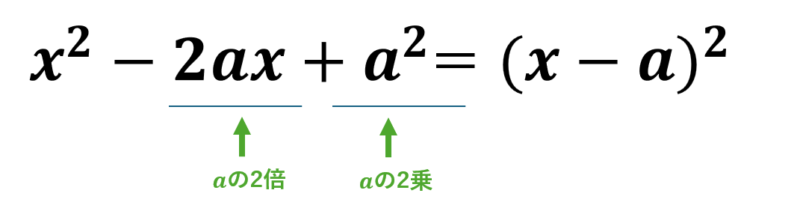
2.の式が-になっただけです。
\( x^2-10x+25 \)を考えてみましょう。
\( 5 \times 2=10、5^2=25 \)ですので、公式を使うことができますね。

\( 4.x^2-a^2 = (x+a)(x-a) \)
2乗どうしの引き算の因数分解です。応用範囲の広い公式です。
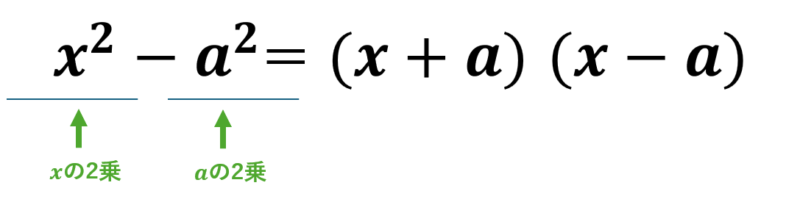
\( x^2-49 \)を考えてみると、49は7の2乗ですので、\( (x+7)(x-7) \)と因数分解できます。
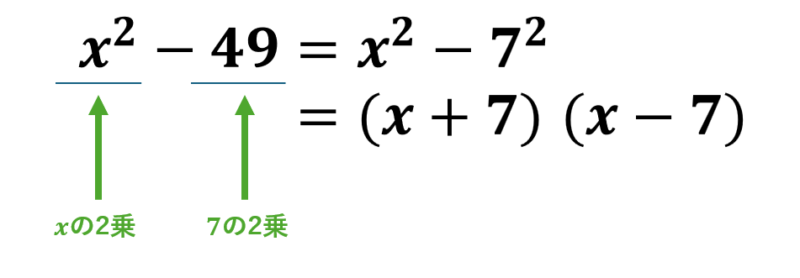
\( x^2-10 \)を考えます。10は2乗になる整数はありませんね。しかし、中3でルートを学ぶと10は\( \sqrt{10} \)の2乗だと扱えます。すると、\( (x+\sqrt{10})(x-\sqrt{10}) \)と計算ができます。
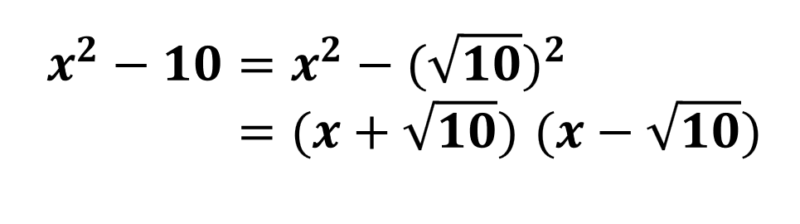
\( x^2-a^2 = (x+a)(x-a) \)の公式は√も含めるとかなり因数分解のしやすい公式だと言えますね。
【応用】③大きな塊を置き変える
少し応用的な方法になります。
同じ塊が見つかった場合は、塊をX(ラージ)のように置き換えることが有効になります。置き換えることで今まで全く分からなかった問題が簡単に見えることがありますので、あきらめずに塊を探してみましょう。
うまくいくと塊で置いた後に、①や②の方針で考えることができます。
2問だけ例題を見てみましょう。
(1)\( (a+b)^2+4(a+b)+4 \)
最初に見た時はぴんと来ないと思います。くくれもしないし、因数分解の公式も使えそうにありません。
こういう時に、「\( a+b \)を一つの大きな文字に置いたらどうだろう?」と考えられると因数分解の計算でできることがぐっと増えます。
じつは\( a+b \)を塊とみて、置き換える(今回はAと置いています)と、②で紹介した因数分解の公式がそのまま使えます。
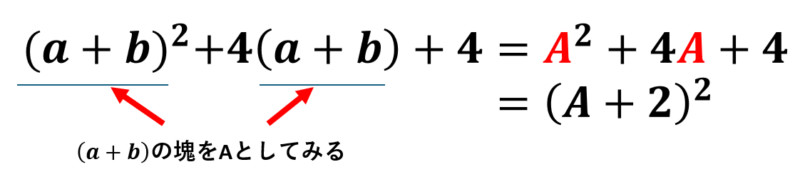
(2)\( a^2(x+y)^3+6b(x+y) \)
こちらもパッと見難しそうで、因数分解(というか数学)が苦手な人は頭が真っ白になるかもしれません。
しかし、こちらも\( x+y \)を一つの塊(今回はXとしてみましょう)とみると、非常に簡単な共通部分をくくる問題に見えると思います。
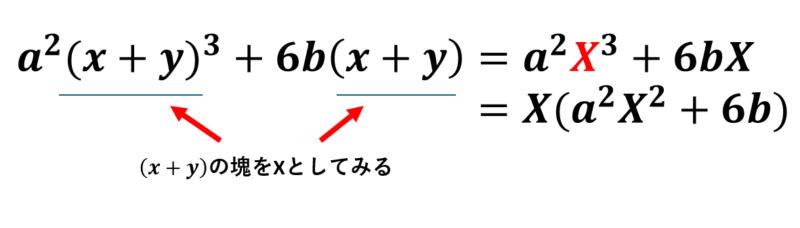
もし、今簡単に見えなくても学校の教科書や問題集で因数分解の練習をすれば、ピンとくる瞬間が訪れるでしょう。
数の組み合わせが全然思いつかない
初めて因数分解を勉強しているひとや計算が苦手な人は
・どの数をくくればいいのかわからない
・因数分解の数の組み合わせが見つからない
と苦労するかもしれません。どのようにすれば数の組み合わせや良いくくり方が見つかるのでしょうか?
残念ながらセンス(感覚)を磨くというのが近道です。
センスといっても生まれながらのものではありません。何問か練習すればどこかのタイミングで「この数字の組み合わせでは?」とわかるようになるものです。
才能は開花させるものですが、センスは磨くものです。

練習問題
このブログの中で練習問題を用意しました。学んだことを確認するためにご活用ください。
まとめ
最後に因数分解のやり方を確認しておきましょう。
①共通部分をくくる
②公式を使う
③大きな塊を見つける
基本的に共通部分をくくることができればくくったほうがスムーズに因数分解できますので、まずはくくれるかどうかを考えてみましょう。
慣れるまではとてもできるようになるとは思えないかもしれませんが、この記事にある公式を見ながら手持ちの問題集で身に付けてください。学校で配布されているもので十分です。すぐにできるようになると思います。
もし手元の問題集がしっくりこなければ簡単な計算ドリルを買ってやれば十分でしょう。
この単元はテストで必ず出るところですので、サクッと計算を身に付けて得点源にしてください。
補足 | 展開公式
復習のために展開公式を載せておきます。ここで展開の公式も学びなおしておくとさらに理解が深まります。
\(
1.(a+b)(c+d)=ac+ad+bc+bd \\
2.(x+a)(x+b)=x^2+(a+b)x+ab \\
3.(x+a)^2=x^2+2ax+b^2 \\
4.(x-a)^2=x^2-2ax+b^2 \\
5.(x+a)(x-a)=x^2-a^2 \\
6.(ax+b)(cx+d)=acx^2+(ad+bc)x+bd \\
\)
気になる方は以下のリンクから記事を読んでいただければよいと思います。