中学数学で苦手になりやすい2次方程式の公式と解き方をまとめました。勉強の際に確認用として活用してくれると嬉しいです。
2次方程式の解き方
①平方根を使う方法
②因数分解を使う方法
③解の公式を使う方法
目次 非表示
① 平方根を使う方法
2次方程式が \(x^2 = a\) の形になっているとき、平方根を使って解くことができます。
\(x = \pm \sqrt{a}\)とできるからです。 \(ax^2 = b\)となっていても、 \(x^2 = \frac{b}{a}\)とできるので、平方根として解くことができます。
例題
$$ x^2 = 16 $$
解答
両辺の平方根をとります。
\( \begin{align*} x^2 &= 16 \\ x &= \pm \sqrt{16} \\ x &= \pm 4 \end{align*} \)
したがって、解は \(x = \pm 4\) です。
② 因数分解を使う方法
2次方程式を因数分解し、積が0になる性質を利用して解く方法です。
$$ AB=0 ならば A=0 または B=0 $$
というルールがあります。因数分解をするとAB=0という形にできるので上のルールで解けます。
例題
\(x^2 – 5x + 6 = 0\) を解きましょう。
解答
左辺を因数分解します。
\( \begin{align*} x^2 – 5x + 6 &= (x – 2)(x – 3) \end{align*} \)
よって、方程式は
\( (x – 2)(x – 3) = 0 \)
となります。先ほどのAB=0の形になりました。
\( (x – 2)(x – 3) = 0 ならば x-2=0 または x-3=0 \)
\( x – 2 = 0 \Rightarrow x = 2 \\ x – 3 = 0 \Rightarrow x = 3 \)
したがって、解は \(x = 2\) と \(x = 3\) です。
③解の公式
2次かい方程式\(ax^2 + bx + c = 0\)(ただし、\(a \neq 0\))の解(\(x\) の値)を一瞬で求めることができます。
因数分解や平方根の解き方と異なり、公式に入れれば一発です。最悪、因数分解も思い浮かばず、平方根も忘れてしまったら雑に解の公式を使いましょう。
$$ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $$
例題
\(2x^2 + 3x – 2 = 0\) を解きましょう。
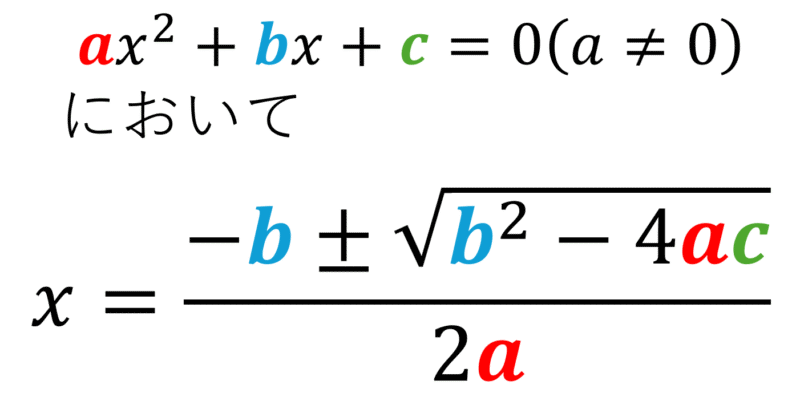
解答
係数を確認します。
\( a = 2,\quad b = 3,\quad c = -2 \)
解の公式に代入します。
\( \begin{align*} x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} &= \frac{ -3 \pm \sqrt{3^2 – 4 \times 2 \times (-2)} }{2 \times 2} \\ &= \frac{ -3 \pm \sqrt{9 + 16} }{4} \\ &= \frac{ -3 \pm \sqrt{25} }{4} \\ &= \frac{ -3 \pm 5 }{4} \end{align*} \)
2つの場合を考えます。
- \(x = \frac{ -3 + 5 }{4} = \frac{2}{4} = \frac{1}{2}\)
- \(x = \frac{ -3 – 5 }{4} = \frac{ -8 }{4} = -2\)
したがって、解は \(x = \frac{1}{2}\) と \(x = -2\) です。
まとめ
今回は2次方程式の解き方をまとめました。2次方程式は中学数学、高校数学共によく使いますのでテストをする際に一気に頭に入れておきましょう




