2次方程式\(ax^2+bx+c=0\space (a\ne0)\)の解（\(x\) の値）を一瞬で求めることができます。
因数分解や平方根の解き方と異なり、公式に入れれば一発です。最強ですね
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
目次 非表示
覚え方
個人的には覚え方も何もない気がするのですが、それではあまりに寂しいので自分が考える覚え方と生成AIが教えてくれた覚え方を載せておきます。
解の公式の覚え方その１（筆者流）
方程式と式を見比べつつ問題を解いて覚えます。色付けをすると対応がわかりやすいですね。
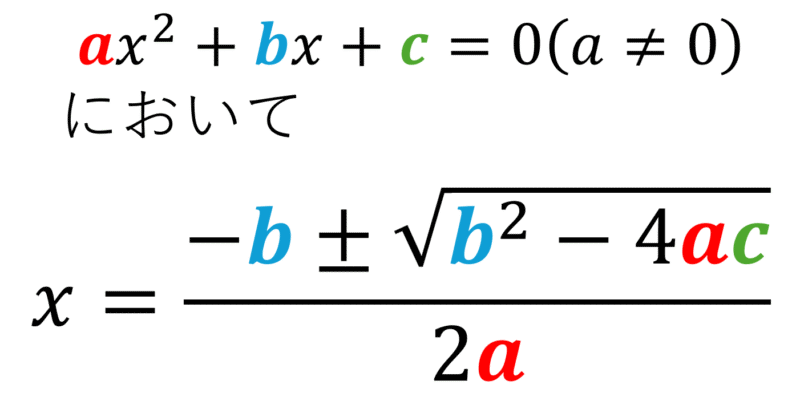
解の公式の覚え方その2（生成AI流）
ChatGPT4-oとGemini1.5proの2つに聞いてみました。
まずはおなじみChatGPT4-o
解の公式を覚えるための簡単な方法があります。次のフレーズを覚えると良いでしょう。
「マイナス B、プラスマイナス、ルートの中に B 二乗マイナス 4AC、全部を 2A で割る」
このフレーズをリズムに合わせて繰り返し唱えることで、自然と公式が頭に入ります。
つづいて、Gemini1.5pro
- マイナスびー
- プラスマイナス ルート
- びーじじょう マイナス よんえーしー
- ぶんの にーえー
リズムに乗せて、何度も口に出してみよう！
声に出して覚えるの好きだなぁ。
と思いつつ、音読が学習効果に与える影響を示す研究を調べたら山のように出てきました。効果あるんだろうなとは思っていましたが、実証研究たくさんあるものですね。
ということで、音読しましょう。
解の公式の使いどころ
2次方程式が苦手な人は、「2次方程式見たらとりあえず解の公式にぶち込む」でいいんじゃないでしょうか？
解の公式の使いどころをもう少し丁寧に説明
先ほどの説明だと理由が書いてありませんし、少し数学ができて2次方程式に苦手意識のない人には参考にならないと思うのでもう少し丁寧に説明することにします
２次方程式は基本的には以下の形になれば楽に解けます。
・因数分解できる形＝０
・（xが入っている式）2=A(定数)
これらができない場合（または、本当はできるけど計算しているときに思いつかなかった場合）は解の公式を使いましょう。
計算は面倒ですし、ミスの確率は上がりますが解けないよりましです。解き終わり、復習をするときにもっと楽な方法で溶けるかどうかを再検討しましょう。
解の公式を用いる例題
それでは、実際に解の公式を用いて2次方程式を解いてみましょう。
例題
次の2次方程式を解の公式で解きなさい。 \( x^2 – 3x + 2 = 0 \)
もしかしたらこの解きかたの方がよくない？」と思う人もいるかもしれませんが、今回は解の公式を使ってみてください。
1.まず、係数 \(a, b, c\) を確認します。
- \(a = 1\)
- \(b = -3\)
- \(c = 2\)
2.次に、解の公式にこれらの値を代入します。
$$ x = \frac{{-(-3) \pm \sqrt{{(-3)^2 – 4 \cdot 1 \cdot 2}}}}{2 \cdot 1} $$
3.計算を進めます。
$$ x = \frac{{3 \pm \sqrt{{9 – 8}}}}{2} $$
$$x = \frac{{3 \pm \sqrt{1}}}{2} $$
$$ x = \frac{{3 \pm 1}}{2} $$
4.最後に、2つの解を求めます。
$$x = \frac{{3 + 1}}{2} = 2 $$
$$ x = \frac{{3 – 1}}{2} = 1$$
したがって、この2次方程式の解は \(x = 2\) と \(x = 1\) です。
復習
問題を解き終わったので、もっと楽に解けなかったかどうかを検討しましょう。
今回の２次方程式の解を見てもらった人はわかるかもしれません。実は、 \(x^2 – 3x + 2 \)は\((x-2)(x-1)\)と因数分解できます。
ということは\((x-2)(x-1)=0\)なので、\((x-2)=0または(x-1)=0\)であるので、２次方程式の解は \(x = 2\) と \(x = 1\)となります。
この場合、因数分解に気が付かなかったのでこちらの解きかたができなかったわけですね。
もし、因数分解が思いつかなかった人はこのタイミングで因数分解の計算練習をしておきましょう。因数分解の技術はできればできる分だけ理系科目の計算を楽にしてくれます。
補足 | 解の公式の派生
解の公式を使う時に、一部式を省略できる可能性がありますよって話です。
2次方程式\(ax^2 + bx + c = 0\)（ただし、\(a \ne 0\)）において、bが偶数の場合、\(b=2b’\)と変更でき、解は以下のように変形することができます。
$$x = \frac{-b’ \pm \sqrt{b’^2 – ac}}{a}$$
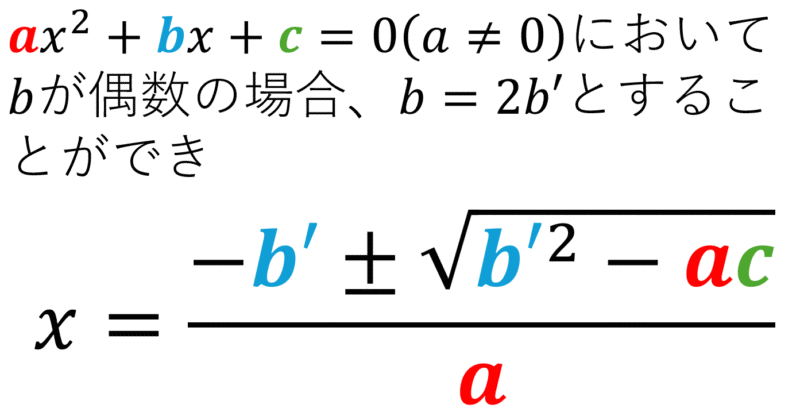
求め方も簡単です。b=2b’を解の公式に入れてみましょう
$$x = \frac{-(2b’) \pm \sqrt{(2b’)^2 – 4ac}}{2a}$$
$$x = \frac{-2b’ \pm \sqrt{4(b’^2 – ac)}}{2a}$$
$$x = \frac{-(2b’) \pm 2 \sqrt{b’^2 – ac}}{2a}$$
$$x = \frac{-b’ \pm \sqrt{b’^2 – ac}}{a}$$
例題
\(3x^2 – 8x + 2 = 0\)の場合、\(-8=-4×2\)となるので、以下の通り計算できます。
$$x = \frac{{-(-4) \pm \sqrt{{(-4)^2 – \cdot 3 \cdot 2}}}}{ 3} $$
$$ x = \frac{{4 \pm \sqrt{{16 – 6}}}}{3} $$]
$$ x = \frac{{4 \pm \sqrt{10}}}{3} $$
