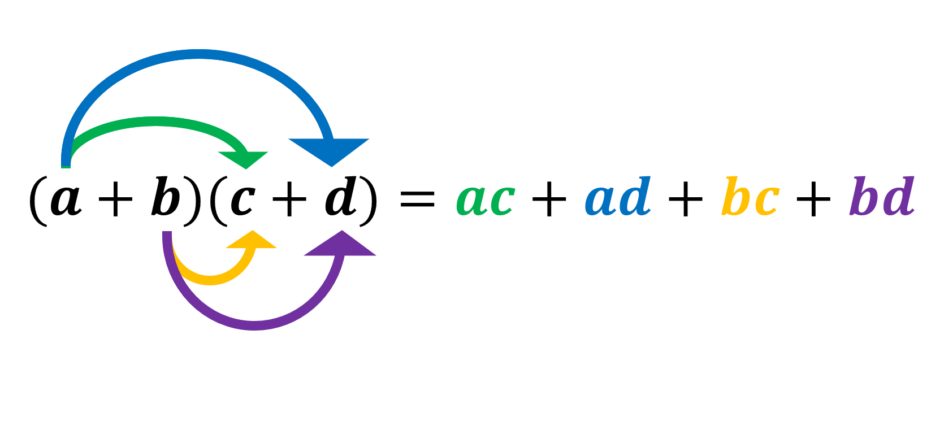この記事では中学数学で習う式の展開の公式をまとめています。公式と覚え方、確認のための例題を一つの記事でコンパクトに確認できるようにしました。ぜひご活用ください。文字式のポイントを一気にまとめた記事もある井ノ出そちらもどうぞ
目次 非表示
展開の公式（乗法公式）
\(\begin{array}{l} 1.(a+b)(c+d)=ac+ad+bc+bd \\2.(x+a)(x+b)=x^2+(a+b)x+ab \\3.(x+a)^2=x^2+2ax+a^2 \\4.(x-a)^2=x^2-2ax+a^2 \\5.(x+a)(x-a)=x^2-a^2 \\ \end{array}\)
ちなみに、こちらは右から見ると因数分解の公式になります。
ポイント
①覚えるのが苦でなければ覚えてしまおう
②もし忘れてしまったら分配法則で解こう
覚えることができて、練習を繰り返せればそれに越したことはありません。しかし、数学が苦手であれば公式を忘れてしまうことがあるかもしれません。その時は②に書いてあるように分配法則（式１）でごり押ししましょう。ごり押しでもスマートに解いてもあっていれば良しと割り切ることも重要です。
分配法則で計算をするときは下の図のようにすべて掛け算をするイメージです。
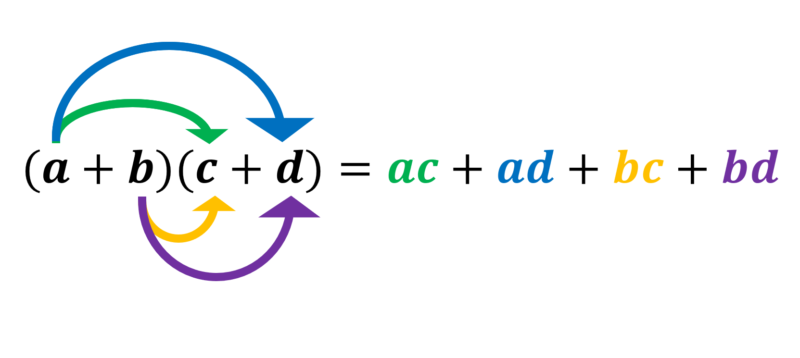
確認問題
\((1)(a+2b)(3c+4d)\)
\((2)(x+2)(x-8)\)
\((3)(x+7)^2\)
\((4)(x-4)^2\)
\((5)(x+3)(x-3)\)
紙とペンを用意して解いてください。解き終わったら解答と解説を読んでください
解答と解説
実は公式に対応しています。改めて確認しましょう。
\begin{array}{l} 1.(a+b)(c+d)=ac+ad+bc+bd \\2.(x+a)(x+b)=x^2+(a+b)x+ab \\3.(x+a)^2=x^2+2ax+a^2 \\4.(x-a)^2=x^2-2ax+a^2 \\5.(x+a)(x-a)=x^2-a^2 \\ \end{array}
では、解答です。
\( \begin{eqnarray}(1) (a+2b)(3c+4d) & = & a \cdot 3c + a \cdot 4d + 2b \cdot 3c + 2b \cdot 4d \\ & = & 3ac + 4ad + 6bc + 8bd \end{eqnarray} \)
\( \begin{eqnarray}(2) (x+2)(x-8) & = & x^2 + (2 – 8)x + 2 \cdot (-8) \\ & = & x^2 – 6x – 16 \\ \end{eqnarray} \)
\( \begin{eqnarray}(3) (x+7)^2 & = & x^2 + 2 \cdot 7 \cdot x + 7^2 \\ & = & x^2 + 14x + 49 \\ \end{eqnarray} \)
\( \begin{eqnarray}(4) (x-4)^2 & = & x^2 – 2 \cdot 4 \cdot x + 4^2 \\ & = & x^2 – 8x + 16 \\ \end{eqnarray} \)
\( \begin{eqnarray}(5) (x+3)(x-3) & = & x^2 – 3^2 \\ & = & x^2 – 9 \\ \end{eqnarray} \)
応用公式
もう一つ展開公式があります。
$$ (ax+b)(cx+d)=acx^2+(ad+bc)x+bd $$
展開をするだけであれば覚える必要はないのですが、後に勉強する因数分解の兼ね合いで覚えておくと便利です。
恐らく高校生の範囲になります。これを聞くとなお覚える必要がありませんね。しかし、進学校だと中学生で習うこともあります。この瞬間だけ進学校気分を味わってください
例題
$$ (2x+6)(3x-5) $$
最悪、公式を覚えてなくても分配法則でいけますよ。解けたら解答と解説を確認してください
では解答と解説。
公式を確認してください。
$$ (ax+b)(cx+d)=acx^2+(ad+bc)x+bd $$
これに当てはめてみると
\begin{array}{l} (2x+6)(3x-5) &=& 2・3x^2+(2・(-5)+6・3)x+6・(-5) \\&=& 6x^2+8x-30 \end{array}
