今後の数学の勉強でよく使う言葉なので確認しましょう
用語解説 | 単項式と多項式とは?
単項式:数、文字式の掛け算と割り算で構成されている式
多項式:単項式の和で構成されている式
なんだか難しいですね。実際の文字式で確認しましょう。以下の式を使います
$$ x^2a+4x+5 $$
+や-で区切られた一つ一つが単項式、集めて多項式
今回の式\(x^2a+4x+5\)で見てみると、+や-で区切られた一つ一つを見ると以下のようになります
\(x^2a\)、\(4x\)、\(5\)
これら一つ一つが単項式です。そして、これらを+や-で集めた式\(x^2a+4x+5\)を多項式といいます。
単項式と多項式の違いでよくある間違い
人によっては「長ければ多項式、短ければ単項式」といった形で考えてしまうかもしれません。しかし、これはやめてください。おそらく間違えるので。
単項式と多項式の違いは足し算や引き算が式の中にあるかどうか
このポイントで理解してください。
単項式と多項式の違いを理解するクイズ
単項式か多項式かを判断するクイズを解いてみましょう。解き終わってから回答と解説を読んでください
$$ x-3a $$
これは、引き算(-)が含まれているので、多項式です。
$$ 3xy $$
これは\( 3 \times x \times y \)と分解でき、すべて掛け算なので単項式です。
$$ \frac{x^2-4x+4}{3} $$
こちらの式は+や-で含まれているので多項式です。
$$ \frac{a^2x}{32b} $$
この式は \( a^2 \) を \( 32b \) で割った形ですが、分子と分母の変数がすべて掛け算または割り算で構成されており、加算や減算が含まれていません。したがって、これは単項式です。
最後は少し難しめです。こちらは単項式でしょうか?多項式でしょうか?
$$ \frac{12345abcdefgxy^2z \alpha}{4566789hijklmnopq \beta} $$
この文字式はめちゃくちゃ長いですね。しかし、単項式です。この式は分解するとこのようになります(長いので横にスクロールしてください)。
$$ \frac{12345abcdefgxy^2z \alpha}{4566789hijklmnopq^4 \beta}=(12345\times a\times b\times c\times d\times e\times f\times g\times x\times y \times y \times z \times \alpha) \div (4566789 \times h \times i \times j\times k\times l\times m\times n\times o\times p\times q\times \beta) $$
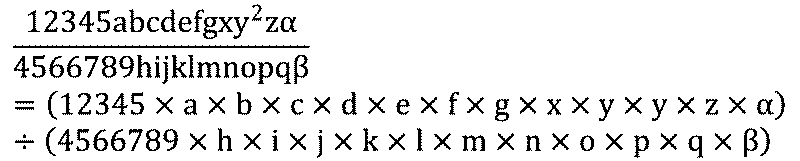
ものすごく長い式ですが、実は掛け算と割り算のみで構成されています。つまり、この式は単項式です。
単項式か多項式かどうかは、式の長さではなく足し算、引き算が含まれているかどうかで判断するということを忘れないでください。
この記事のほかにも数学のまとめに役立つ記事を書いているのでよかったら参考にしてください