①一つの弧に対する円周角の大きさは一定(同じ)である
②中心角は円周角の2倍
③円周角が等しい⇔弧が等しい
④円周角の定理の逆
①一つの弧に対する円周角の大きさは一定(同じ)である
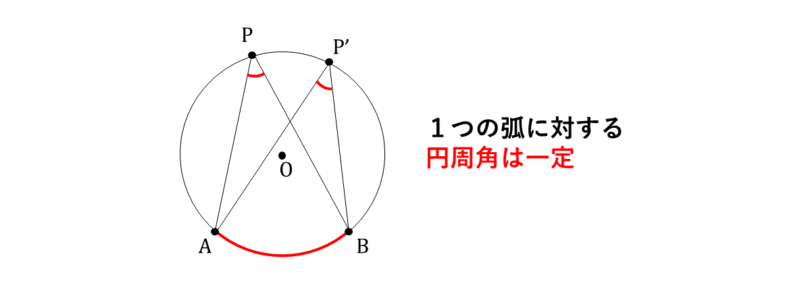
1つの弧を固定して円周角を作ると角度が一定になります。
$$ \angle APB = \angle AP’B $$
try it より
同じ弧 \(\widehat{AB}\) に対して、円周上の任意の点 \(P\) をとると、 円周角 \(\angle APB\) はどの位置に \(P\) を置いても等しくなります。 つまり、同じ弧\( \widehat{AB} \)に対して、\( \angle APB \)は一定の値をとる。
角度の計算や証明などあらゆる図形の問題で使います。
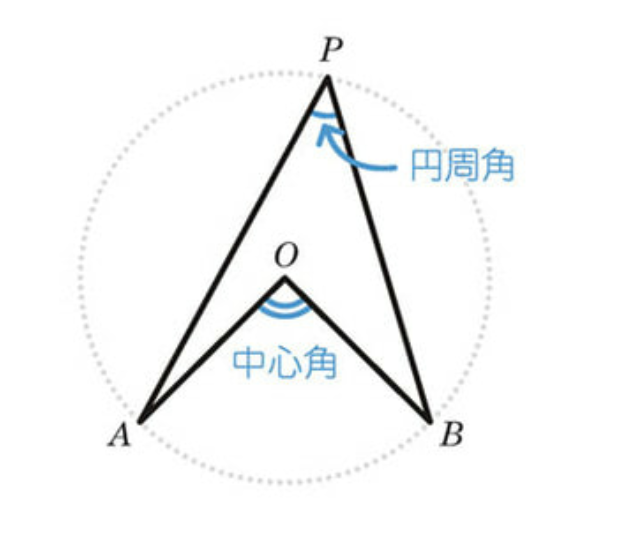
②1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である
\(\widehat{AB}\) に対する中心角を \(\angle AOB\) (ここで \(O\) は円の中心) とすると、 対応する円周角 \(\angle APB\) はその半分になります。
$$ \angle APB = \frac{1}{2} \angle AOB $$
改訂版 中学校3年間の数学が1冊でしっかりわかる本より
この公式を応用すると、直径の円周角は90°(直角)になります.
wikipediaより
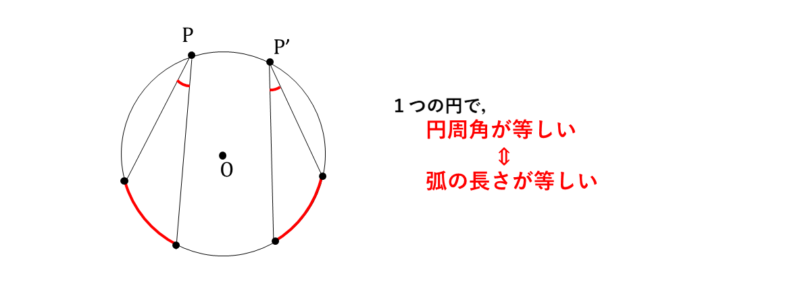
③円周角が等しい⇔弧が等しい
2つの弧 \(\widehat{AB}\) と \(\widehat{A’B’}\) に対する円周角が等しいならば、 それらの弧は等しい弧となります。逆に等しい弧に対してつくられる円周角は等しくなります。
$$ \angle ACB = \angle A’C’B’ \iff \widehat{AB} = \widehat{A’B’} $$
try it より
④ある角が一定の値を保つとき、その頂点を通る円が存在する(円周角の定理の逆)
以下に、点を使った説明も記載しておきます
4点 \( A,B,C,D \)について,2点 \(C,D \) が直線 \( AB \) について同じ側にあり,\( \angle ACB= \angle ADB \)であるならば,4点 \( A,B,C,D \) は同一円周上にある。
文章にすると円周角が一定であれば、その頂点は円周上にあることが示せるということです。 つまり、「ある角が一定の値を保つとき、その頂点を通る円が存在する」という事実が円周角の定理の逆として成立します。