目次 非表示
おうぎ形の弧の長さと面積の公式
1. 弧の長さの公式
おうぎ形の弧の長さ l は、次の公式で求められます:
\( l = r \times 2\pi \times \frac{a(中心角)}{360} \)
ここで、r は円の半径です。
2. 面積の公式
おうぎ形の面積 A は、次の公式で表されます:
\( A = r^2 \times \pi \ \frac{a(中心角)}{360} \)
同様に、r は半径です
解説図と覚え方
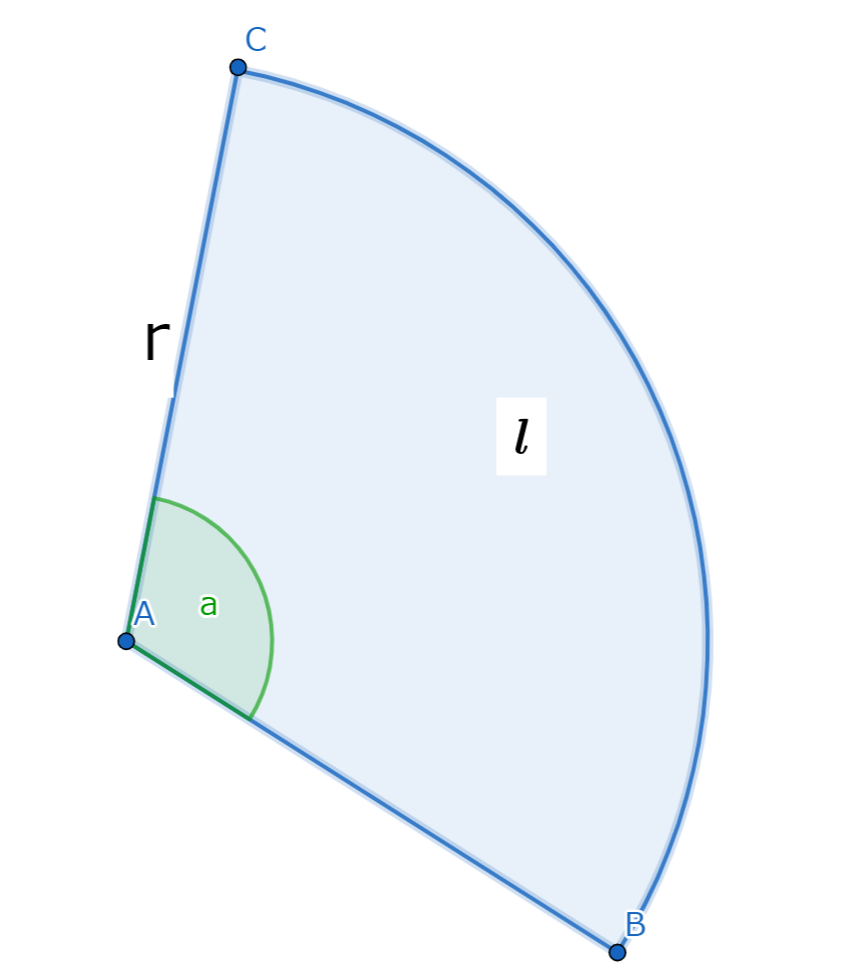
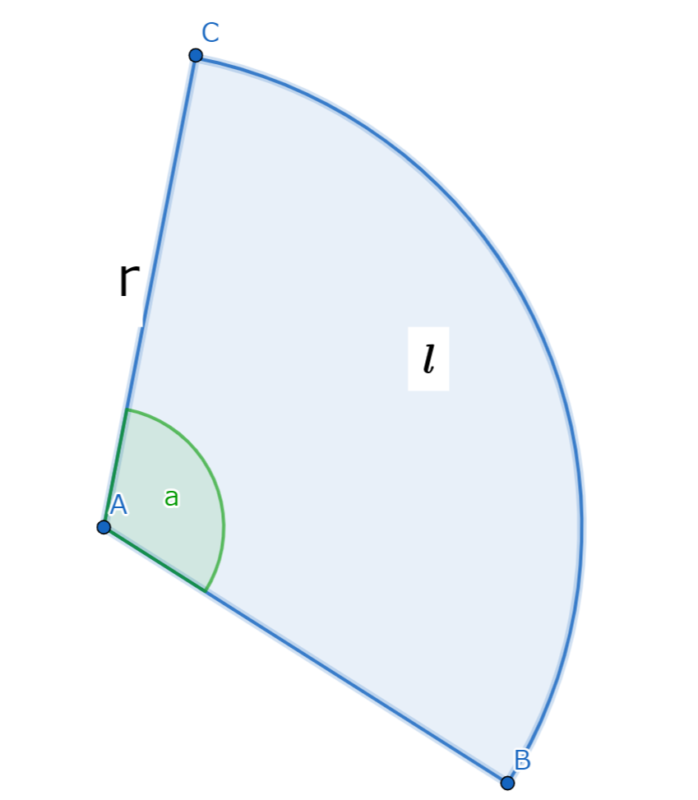
上記の図は、おうぎ形(扇形)を示しています。中心角 \( \theta \)、半径 r、弧の長さ \( l \) が図示されており、面積もその内部に示されています。
弧の長さ、面積共に「円周に角度 \( \frac{a(中心角)}{360} \) を掛ける」、「円の面積に角度 \( \frac{a(中心角)}{360} \) を掛ける」だけなのでシンプルに覚えられます。
例題
問題
半径 r=3 cm、中心角 120° のおうぎ形の弧の長さと面積を求めなさい。
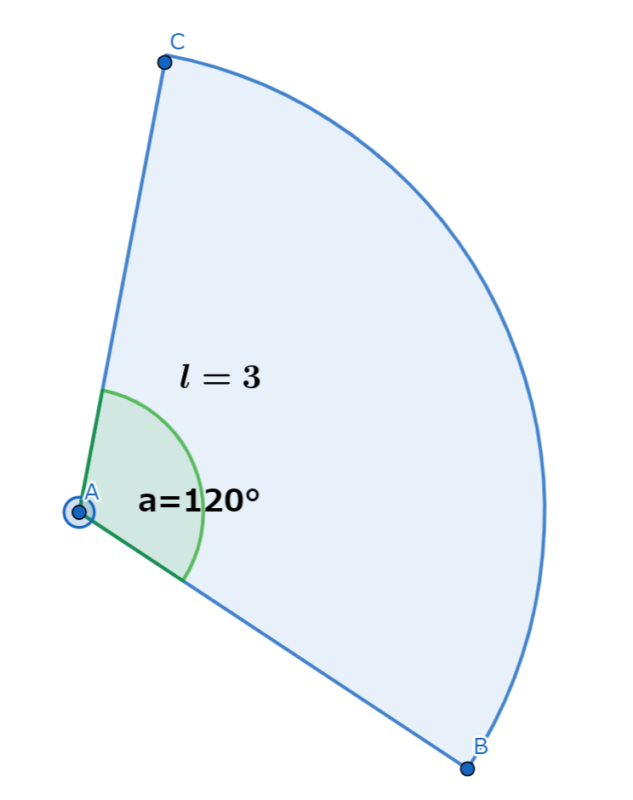
解答:
弧の長さ l:
$$ \begin{align*} l &= 3 \times 2\pi \times \frac{120}{360} &=6\pi \times \frac{1}{3} \pi &=2 \pi \end{align*}$$
面積 A:
$$ \begin{align*} A &= 3^2 \times \pi \ \frac{120}{360}&=9\pi \times \frac{1}{3} \pi &=3 \pi \end{align*}$$
扇形の面積を求めるもう一つの公式
\( A = r \times l \times \frac{1}{2} \)
弧の長さを使って求めることもできます。