この記事では高校数学の範囲で学ぶ加法定理とそこから派生する諸公式をまとめ、証明を示します。
加法定理の証明が東大の入試に出たことが注目を集めているので証明が気になる人もいると思います。公式と証明は教科書に載っているものの、証明方法と公式覚え方を一気に見たいということも多いと思います。
三角関数の中で最も重要な公式の一つですので公式と証明をこの記事で都度確認してください。
加法定理
\(
\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \quad (a) \\
\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \quad (b) \\
\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \quad (c)
\)
覚え方
\( sinとcos \)は「しここし、ここしし、こしたんたん」とでも覚えておけばよいのではないしょうか。\( tan \)は「1ひくタンタン分のタンプラタン」とかですかね?覚え方は任せます。
ゴロで覚えて問題を解いて定着させましょう。
加法定理の証明
東大の入試にも出たことで非常に有名になった証明ですね。

教科書に書いてあるレベルの問題を入試で出したということで、当時の受験生にとって衝撃的なだったそうで、物議をかもしました。しかも、東大受験生という日本で一番頭の良い高校生を集めた試験にもかかわらず正答率は2割程度ともいわれています。
東大の入試も出たほどですが、方法は非常にシンプルなので証明の流れを見ていきましょう。
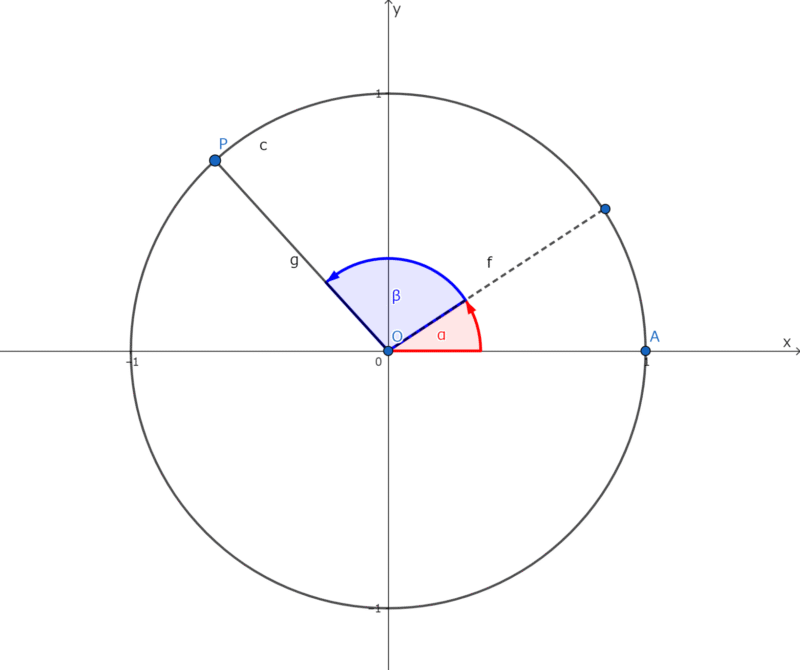
下図のように単位円周上に\(点A(1,0)、点P(\cos(\alpha + \beta),\sin(\alpha + \beta))\)を取ると、APは下記式のように示される。
\(
AP^2=\sin^2 (\alpha + \beta)+\{1-\cos (\alpha + \beta)\}^2\\
=2-2 \cos (\alpha + \beta)…①\\
(∵\sin^2 (\alpha + \beta)+\cos^2 (\alpha + \beta)=1)
\)
続いて、下記図のように、点A,Pを原点を中心に\(-\alpha\)回転させた点をA’,P’とする。
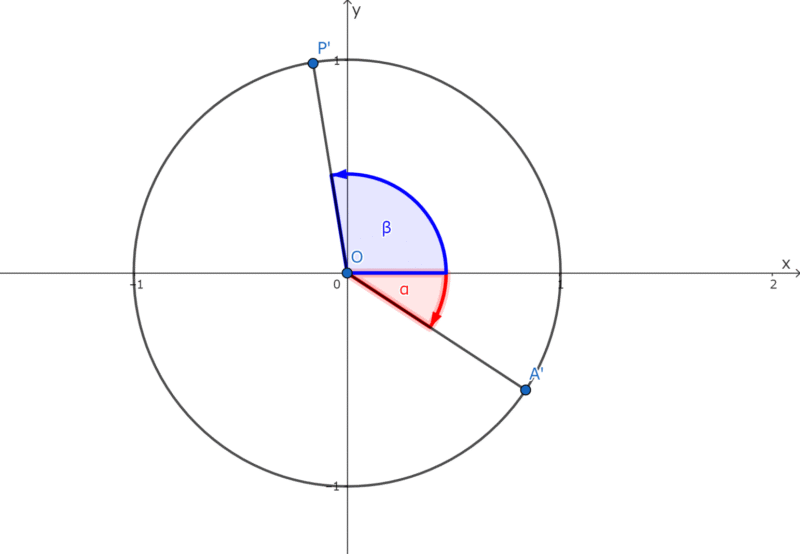
この時、A’,P’は\(A’(\cos \alpha, -\sin \alpha)、点P’(\cos \beta, \sin \beta)\)と表されるため、下記式として表される。
\(
A’P’^2=(\cos \beta- \cos \alpha)^2+(\sin \beta + \sin \alpha)^2 \\
=2-2(\cos \beta \cos \alpha- \sin \alpha \sin \beta )・・・②
\)
AP=A’P’より①=②となるから、\(\cos(\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta…③\)が示される。
あとは\(\betaを-\beta、\alphaを\frac{\pi}{2} \pm\alpha\)に変更すると残りがすべて導ける。
ここで、③において\(\betaを-\beta\)とすると、
\(
\cos(\alpha – \beta) = \cos \alpha \cos (-\beta) – \sin \alpha \sin (-\beta)\\
=\cos \alpha \cos \beta + \sin \alpha \sin \beta…④
\)
が導き出せる。(∵三角関数の還元公式より)
また、③において\(\alphaを\frac{\pi}{2} \pm\alpha\)と変形すると、三角関数の還元公式\(\cos \frac{\pi}{2} \pm\theta=\mp \sin \theta、\sin \frac{\pi}{2} \pm\theta= \cos \theta\)より
\(
\text{(③にて }\frac{\pi}{2} +\alpha\text{とする)} \\
\text{(③の左辺)} \\
\cos\left(\frac{\pi}{2} + \alpha + \beta\right) = \cos\left(\frac{\pi}{2} + (\alpha + \beta)\right) \\
\quad = -\sin(\alpha + \beta) \\
\text{(③の右辺)} \\
\cos\left(\frac{\pi}{2} + \alpha\right) \cos \beta – \sin\left(\frac{\pi}{2} + \alpha\right) \sin \beta \\
\quad = -\sin \alpha \cos \beta – \cos \alpha \sin \beta \\
\text{∴ } \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \quad \text{…⑤} \\
\text{(③にて }\frac{\pi}{2} -\alpha\text{とする)} \\
\text{(③の左辺)} \\
\cos\left(\frac{\pi}{2} – \alpha + \beta\right) = \cos\left(\frac{\pi}{2} – (\alpha – \beta)\right) \\
\quad = \sin(\alpha – \beta) \\
\text{(③の右辺)} \\
\cos\left(\frac{\pi}{2} – \alpha\right) \cos \beta – \sin\left(\frac{\pi}{2} – \alpha\right) \sin \beta \\
\quad = \sin \alpha \cos \beta – \cos \alpha \sin \beta \\
\text{∴ } \sin(\alpha – \beta) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \quad \text{…⑥}
\)
tanについては定義より、③~⑥を用いると、
\(
\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta\\
\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \cos \beta\\
\tan(\alpha \pm \beta) = \frac{\sin(\alpha \pm \beta)}{\cos(\alpha \pm \beta)}\\
=\frac{\sin \alpha \cos \beta \pm \cos \alpha \sin \beta}{\cos \alpha \cos \beta \mp \sin \alpha \cos \beta}…(*)\\
\)
分母分子共に\( \cos \alpha \cos \beta \)で割ると、
\(
(*)=\frac{\frac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta} \pm \frac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{1 \mp \frac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}}\\\\
=\frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}\\\\
(\text{∵} \tan x=\frac{\sin x}{\cos x})\\
\)
これで加法定理が示されました。
余弦定理を用いた加法定理の証明
\(\cos (\alpha – \beta)\)を余弦定理によって求める方法もあります。
下図の三角形OPQを考える。PQを余弦定理を用いて表すと、
\(
PQ^2=OP^2+OQ^2-2OP・OQ \cos (\alpha- \beta)\\
=1^2+1^2-2・1・1\cos (\alpha- \beta)\\
=2-2\cos (\alpha- \beta)…①’
\)
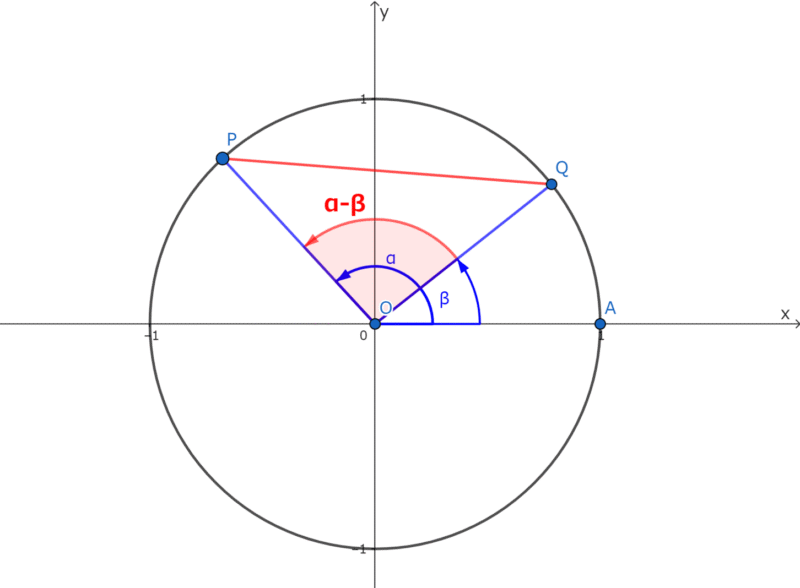
点P,Qはそれぞれ、\(P(\cos \alpha, \sin \alpha),Q(\cos \beta, \sin \beta)\)であることから、
\(
PQ^2=(\cos \beta- \cos \alpha)^2+(\sin \beta + \sin \alpha)^2\\
=2-2(\cos \beta \cos \alpha- \sin \alpha \sin \beta )…②’
\)
①’=②’より、
\(
2-2\cos (\alpha- \beta)=2-2(\cos \beta \cos \alpha – \sin \alpha \sin \beta )\\
\text{∴ } \cos(\alpha – \beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta
\)
が導き出せる。
これ以降は上記の④以降を求めたのと同じように\(\betaを-\beta、\alphaを\frac{\pi}{2} \pm\alpha\)とすると求めることができます。
加法定理の暗記量は実は少ない
ここまで見てもらった人は加法定理の暗記量が非常に少ないことがわかると思います。証明に示したように、公式の(a)、(b)のどれか一つを覚えてさえいれば、三角関数の還元公式から一発で導けます。重要公式を覚える労力が少ないというのはありがたいものですね。
2倍角の方式
\(
\begin{align*}
\sin2 \theta&= 2 \sin \theta\cos \theta\\
\cos2 \theta &= \cos^2 \theta- \sin^2 \theta\\
& = 2 \cos^2 \theta- 1 \\
& = 1 – 2 \sin^2 \theta\\
\tan2 \theta&= \frac{2 \tan \theta}{1 – \tan^2 \theta}
\end{align*}
\)
2倍角の公式の覚え方と証明
式(a)~(c)の\(\alpha+\beta\)を\(\theta+\theta\)と変更してみましょう。覚えなくても導くことができます。せっかくなので証明のプロセスを下に示しておきます。
式(a)~(c)において\(\alpha=\beta=\theta\)と置くと、
\(
\begin{align*}
\sin 2\theta &=\sin(\theta + \theta) \\
& = \sin \theta \cos \theta+ \cos \theta \sin \theta\\
& =2 \sin \theta \cos \theta…⑦\\\\
\cos 2\theta & =\cos(\theta + \theta) \\
& = \cos \theta \cos \theta – \sin \theta \sin \theta \\
& = \cos^2 \theta- \sin^2 \theta\\
& = 2 \cos^2 \theta – 1…⑧ \\
& = 1 – 2 \sin^2 \theta…⑨\\\\
\tan 2\theta= \tan(\theta + \theta) &= \frac{\tan \theta+ \tan \theta}{1 – \tan \theta \tan \theta}\\
& = \frac{2 \tan \theta}{1 – \tan^2 \theta}…⑩
\end{align*}
\)
半角の公式
\(
\sin^2 \frac{\theta}{2} = \frac{1 – \cos \theta}{2} \\
\cos^2 \frac{\theta}{2} = \frac{1 + \cos \theta}{2} \\
\sin \frac{\theta}{2} \cos \frac{\theta}{2}= \frac{1}{2} \sin \theta \\
\tan^2 \frac{\theta}{2} = \frac{1 – \cos \theta}{1 + \cos \theta}
\)
覚え方と証明
これは倍角の公式から簡単に求めることができます。\(\theta\)を\(\frac{\theta}{2}\)とします。
式⑦~⑨及び\(\tan^2 \theta\)において、\(\theta\)を\(\frac{\theta}{2}\)と変化させると、
\(
\begin{align*}
&\sin 2・\frac{\theta}{2} =2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}\\
&\text{∴ } \sin \frac{\theta}{2} \cos \frac{\theta}{2}= \frac{1}{2} \sin \theta\\\\
&\cos 2・\frac{\theta}{2}= 2 \cos^2 \frac{\theta}{2} – 1 \\
&\text{∴ } \cos \theta+1 = 2 \cos^2 \frac{\theta}{2} \\
&\text{∴ } \cos^2 \frac{\theta}{2} = \frac{1 + \cos \theta}{2} \\\\
&\cos 2・\frac{\theta}{2}= 1 – 2 \sin^2 \frac{\theta}{2}\\\\
&\text{∴ } 2 \sin^2 \frac{\theta}{2}= 1 -\cos 2・\frac{\theta}{2}\\
&\text{∴ } \sin^2 \frac{\theta}{2} = \frac{1 – \cos \theta}{2}\\\\
\tan^2 \frac{\theta}{2} & = \frac{\sin^2 \frac{\theta}{2}}{\cos^2 \frac{\theta}{2}}\\
&=\frac{\frac{1 + \cos \theta}{2}}{\frac{1 – \cos \theta}{2}}\\
&=\frac{1 – \cos \theta}{1 + \cos \theta}
\end{align*}
\)
積和公式
\(
\begin{align*}
\sin x\cos y &=\frac{1}{2}\{\sin(x+y)+ \sin(x-y)\}\\\\
\cos x\sin y &=\frac{1}{2}\{\sin(x+y)- \sin(x-y)\}\\\\
\cos x\cos y &=\frac{1}{2}\{\cos(x+y)+ \cos(x+y)\}\\\\
\sin x\sin y &=-\frac{1}{2}\{\cos(x-y)- \cos(x+y)\}\\\\
\end{align*}
\)
積和公式の覚え方と証明方法
加法定理の両辺を足すことで求めることができます。
\(
\begin{align*}
\begin{cases}
&\sin(x + y) = \sin x \cos y + \cos x \sin y…(a.1)\\
&\sin(x – y) = \sin x \cos y – \cos x \sin y…(a.2)\\
\end{cases}\\\\
\begin{cases}
&\cos(x + y) = \cos x \cos y – \sin x \sin y…(b.1)\\
&\cos(x – y) = \cos x \cos y + \sin x \sin y…(b.2)\\
\end{cases}
\end{align*}
\)
において、(a.1)+(a.2)、(a.1) – (a.2)、(b.1)+(b.2)、(b.1) – (b.2)を行うと、
\(
\begin{align*}
&(a.1)+(a.2) \\
&\iff \sin(x + y) + \sin(x – y) = 2 \sin x \cos y \\\\
&(a.1)-(a.2) \\
&\iff \sin(x + y) – \sin(x – y) = 2 \cos x \sin y \\\\
&(b.1)+(b.2) \\
&\iff \cos(x + y) + \cos(x – y) =2 \cos x \cos y \\\\
&(b.1)-(b.2) \\
&\iff \cos(x + y) – \cos(x – y) = – 2 \sin x \sin y \\\\
\end{align*}
\)
よって、積和公式
\(
\sin x\cos y=\frac{1}{2}\{\sin(x+y)+ \sin(x-y)\} \\
\cos x\sin y=\frac{1}{2}\{\sin(x+y)- \sin(x-y)\} \\
\cos x\cos y=\frac{1}{2}\{\cos(x+y)+ \cos(x+y)\} \\
\sin x\sin y=-\frac{1}{2}\{\cos(x-y)- \cos(x+y)\} \\
\)
が導き出せる。
和積公式
\(
\begin{align*}\sin A + \sin B &= 2\sin \frac{A+B}{2}\cos \frac{A-B}{2} \\\\
\sin A – \sin B &= 2\cos \frac{A+B}{2}\sin \frac{A-B}{2} \\\\
\cos A + \cos B &= 2\cos \frac{A+B}{2}\cos \frac{A-B}{2} \\\\
\cos A – \cos B &= 2\sin \frac{A+B}{2}\sin \frac{A-B}{2} \\\\
\end{align*}
\)
和積公式の覚え方と証明
積和公式にて\(x+y=A、x-y=B\)と置きます。これをxとyについて解くと、\(x=\frac{A+B}{2} , y=\frac{A-B}{2}\)となります。このxとyを積和公式に代入すると、そのまま和積公式が求められます。
まとめ
今回は高校数学(おそらく数Ⅱ)の重要分野の一つである加法定理と派生公式の覚え方と証明方法を整理しました。
公式を忘れたら都度覚え、証明を確認することで定着すると思います。あとは問題演習です。解説の詳しい問題集をやることで加法定理が自分の物になると思います。
補足 三角関数の重要公式
加法定理を証明したり、派生公式を導き出すときに便利な公式も載せておきます。ここまで載せると、加法定理の説明というよりは三角関数のまとめになってしまいますが、まとめなんてなんぼあってもいいですからね。
三角関数の還元公式
加法定理の証明をするときによく使います。
\(
\cos (\frac{\pi}{2} \pm\theta)=\mp \sin \theta , \sin (\frac{\pi}{2} \pm\theta)= \cos \theta , \tan (\frac{\pi}{2} \pm\theta)=\mp \dfrac{1}{\tan \theta} \\\\
\cos (\pi \pm \theta)=\pm \cos \theta, \sin (\pi \pm \theta)= \mp \sin \theta ,\tan (\pi \pm \theta)=\pm \tan \theta \\\\
\)
三角関数の性質
\(
\cos^2 \theta + \sin^2 \theta=1
\)
要は三平方の定理です。加法定理の証明に100回は出てきます。確認しておいてください







