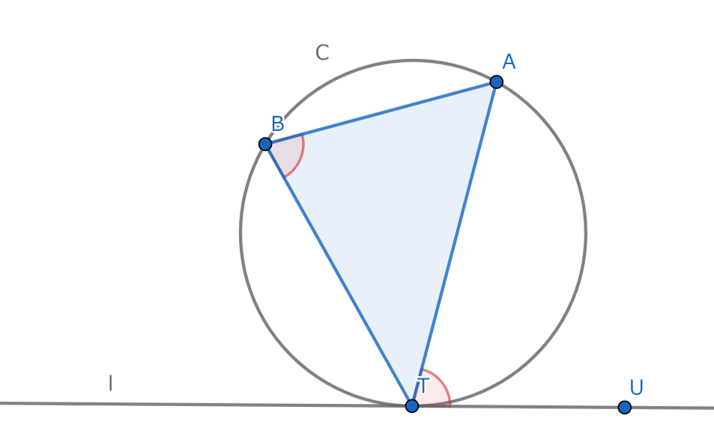
今回は数学Aで習う接弦定理です。円、内接する三角形が出たら必ず出番が来る公式ですのでこの記事で覚えてください。
図を下記ながら記事を読むとすぐに覚えられると思います。今すぐに紙とペンを用意してこの記事の図を描きながら読んでください
目次 非表示
接弦定理の公式と覚え方
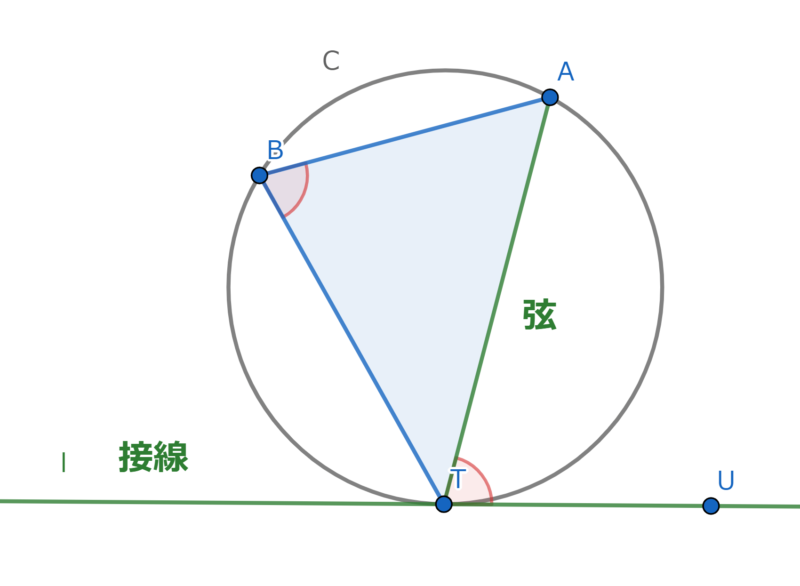
接線と弦のつくる角\(\angle ATU\)は、その弦に対する円周角\(\angle ABT\)と等しい。これを接弦定理(せつげんていり) と言います。
$$ \angle ABT = \angle ATU $$
接弦定理の覚え方
覚え方は図と対応させます。弦を基準に、弦の反対側の角と弦によってできた角として覚える分かりやすいかも。
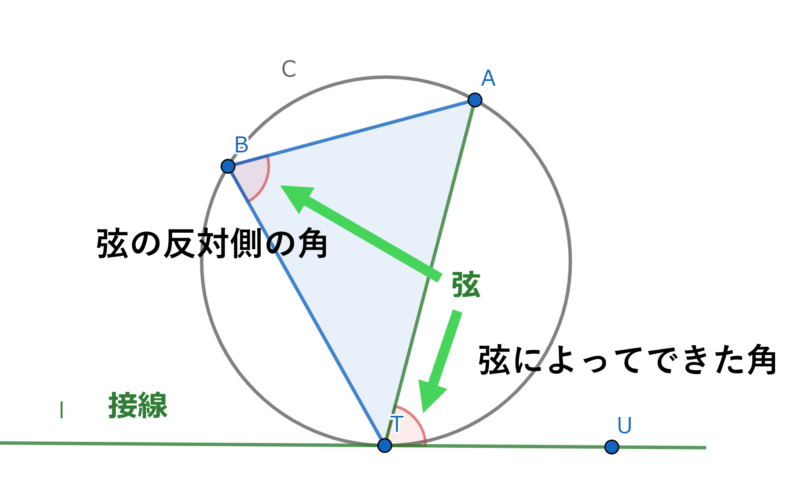
もちろん、数学が得意な人からすれば全く本質的ではないです。でも一度覚えることができればあとは何とでもなります。
もし私が示した覚え方でしっくりこなければ、じぶんにとってピタッと来る覚え方を探してみてください。
接弦定理を拡張させてみる
この接弦定理、下図でいうとオレンジ色の部分にも適用できます。

「そりゃそうだろう」といわれそうですが、そのおかげで、下の式のように2つの接弦定理を見つけることができます。
∠ABT =∠ATU\\ ∠BTR=∠BAT
例題
図において、\(\angle ABT=73^\circ \)、\(\angle BTR=60^\circ\) であるとき、\(\angle BAT\)、\(\angle ATU\) を計算せよ

公式を確認するだけです。忘れてしまったら、もう一度公式を紙に書いて、確認しながら問題を解いてください。
解答
\(
\angle ABT = \angle ATU \\
\angle BTR = \angle BAT
\)
ですので、\(\angle BAT=\angle BTR=60^\circ\)、\(\angle ATU=\angle ABT=73^\circ\)と計算できます。
角度が等しい場所の対応が分かればすぐに解けますね。
最後に
今回は図を豊富に用意して、図をたくさん描きながらこの記事を読んだので、公式と角度の対応関係が頭に入ったと思います。え、流し読みをした?今すぐに紙をペンを用意して図を描きながらこの記事を読み直してください。いいね。
後はたくさん問題を解いて練習してください。問題はあなたが学校でもらった問題集で良いと思います。