【中２、中３数学】関数の変化の割合とは？グラフと実例で理解する

2次関数の変化の割合は、$ x $ の値が増加するにつれて $ y $ の値がどのように変化するかを示します。

式にすると以下のように表すことができます。

$$ \begin{align*} 変化の割合 &= \frac{yの変化量}{xの変化量} \\ &= \frac{y_2 – y_1}{x_2 – x_1} \end{align*} $$

中学２年生の時に初めて習う公式（というか考え方）ですね。しかし、この考え方は中３でも使いますし、高校生になっても、大学生になっても使います。

中学2年生までで習った$ y=ax+b $のようにグラフが直線になる関数では、変化の割合は常に一定です。しかし、二次関数のように直線にならない関数では、変化の割合が入力値の範囲に応じて変わることが特徴です。

参考：【中3数学】2次関数y=ax^2のグラフの描き方と重要ポイントまとめ | 変化の割合の計算方法もまとめました！

11月 2, 2024 【中3数学】2次関数y=ax^2のグラフの描き方と重要ポイントまとめ | 変化の割合の計算方法もまとめました！

目次非表示

中２での変化の割合
中３での変化の割合
変化の割合って何に使うの？
- 実例その１：長期目線で見た時
- 実例その２：短期目線で見た時
最後に
参考文献（GDPのデータ）

中２での変化の割合

中学２年生では、「変化の割合=直線の傾き」として学びます。関数 $ y=ax+by $ の形では、変化の割合は常に一定で、式の $ a $ に対応します。これは、任意の2点をとっても、直線の傾きが変わらないためです。

例えば、$ y=2x+3y $ という関数の場合、$ x $ が1増加すると $ y $ は2増加します。この「2」が変化の割合です。この性質を使うと、グラフが直線になる関数について、関数の式を簡単に導き出すことができます。

中学２年生の時点では、直線グラフを描く練習や、変化の割合を計算してグラフの傾きを理解することが中心となります。

中３での変化の割合

中学３年生では、一次関数から二次関数へと学びが広がります。二次関数 $ y=ax^2+bx+c$では、グラフが放物線になるため、変化の割合は一定ではなく、範囲によって変わります。

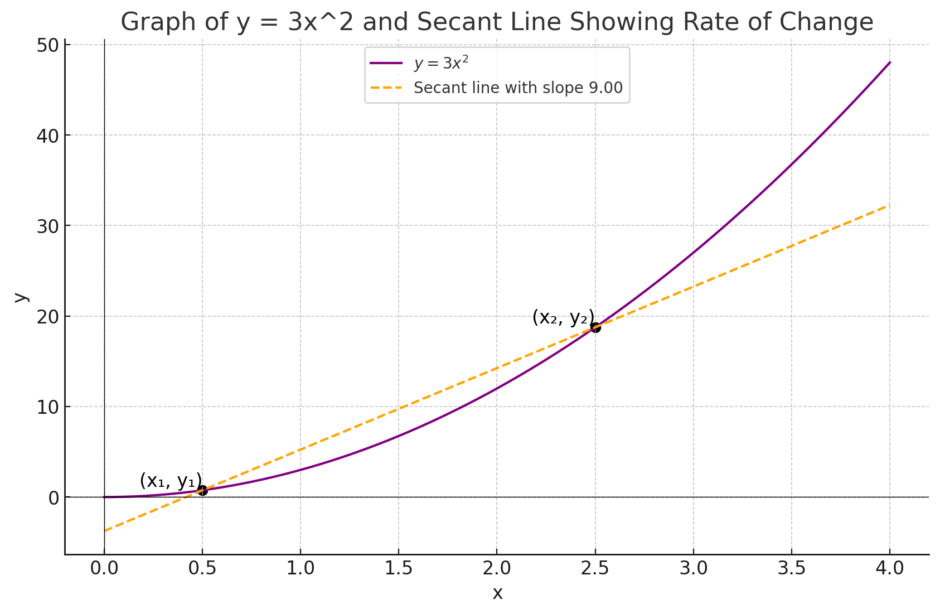
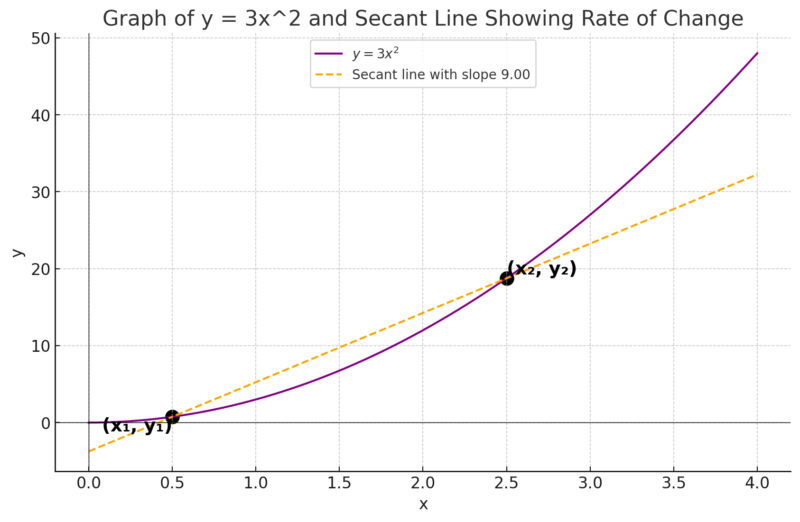
例えば、二次関数\( y = 3x^2) の場合を見てみましょう。

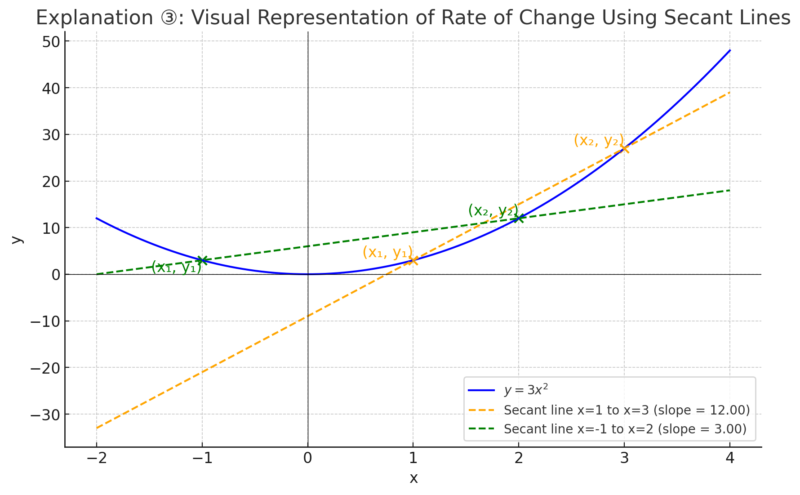
2次関数変化の割合とセカント線 — 2次関数とセカント線。グラフの黄色の点線と緑の点線がセカント線を表しています

青色の曲線は二次関数 $ y = 3x^2 $です。

黄色の点線と緑の点線の傾きが変化の割合を表しています。直線と異なり、直線以外では選ぶ点によって変化に割合が異なることがわかるでしょう。

中３では、変化の割合を使って、放物線の特徴や曲がり方を分析する練習を行います。図形などともからめると非常に応用範囲が広いです。

変化の割合って何に使うの？

変化の割合は、数学の問題だけでなく、日常生活や社会の中で幅広く応用されています。以下にその例を示します。

実例その１：長期目線で見た時

長期的なデータを見るとき、変化の割合を使うことで、全体の傾向を把握することができます。例えば、日本のGDP（国内総生産）のデータを用いて、以下の期間の変化の割合を計算してみましょう。

1960年から1990年のGDP増加率
1990年から2020年のGDP増加率

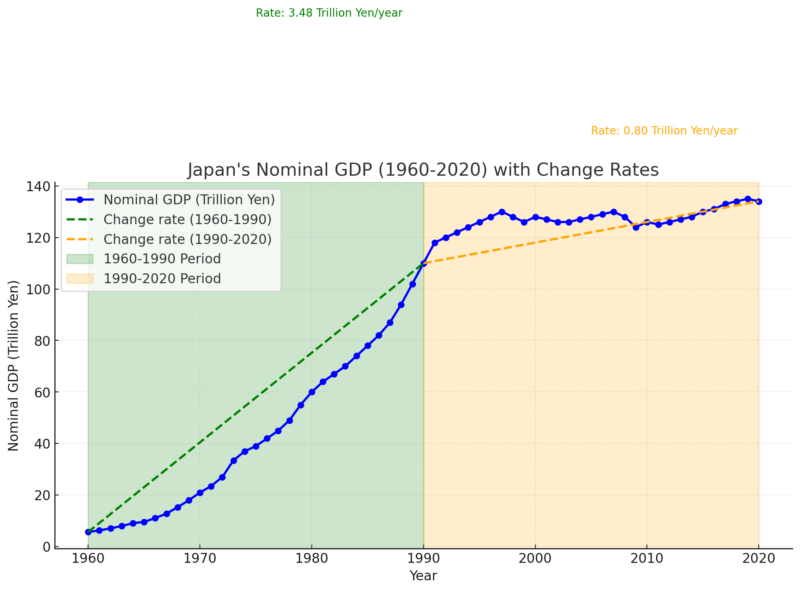
上のグラフを見てください。日本の名目GDP（1960-2020年）と各期間の変化の割合を示しています。

緑の点線: Change rate (1960-1990)
オレンジの点線: Change rate (1990-2020)
各期間の成長率は「Trillion Yen/year」で表記されています。

1960年から1990年の間、日本は高度経済成長期を迎えており、GDPが大幅に上昇しました。一方、1990年から2020年の間はバブル崩壊後の低成長期で、変化の割合（緑とオレンジの点線）は大きく低下しました。このように、変化の割合を計算することで、経済の動きを客観的に理解できます。

実例その２：短期目線で見た時

短期的なデータでは、変化の割合を用いて急激な変化を把握できます。たとえば、YouTubeやSNSでの「急上昇トレンド」は、直近の視聴数やエンゲージメント数の変化の割合に基づいています。

短期的なデータでは、変化の割合を用いて急激な変化を把握することができます。たとえば、YouTubeの「急上昇トレンド」では、単純な再生回数だけでなく、直近の視聴速度（再生回数の増加ペース）がランキングの順位に大きく影響しています。以下の画像で考えてみましょう。

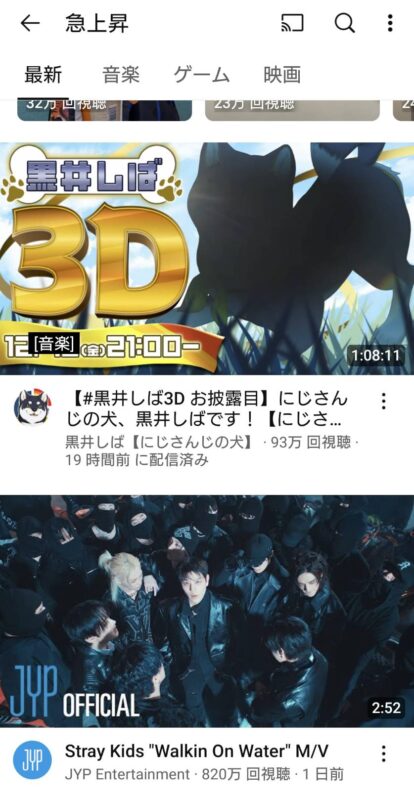
画像にある2つの動画を例に説明します。黒井しばの3D動画: この動画は公開から19時間で93万回再生されています。 Stray Kidsのミュージックビデオ: こちらの動画は総再生回数が820万回です。一見、Stray Kidsのミュージックビデオの方が視聴数が多いにもかかわらず、急上昇のランキングでは黒井しばの3D動画の下になっています。

これは直近の視聴数の変化の割合が黒井しばの3D動画の方が大きいと考えることができます。仮に直近のStray Kidsのミュージックビデオの動画が19時間では60万回再生と仮定します（実際は違う数値だと思いますが、計算のためなので悪しからず）。

この場合、両動画の「再生速度（変化の割合）」を比較してみます。

黒井しばの3D動画の変化の割合

$$ \frac{93{万回}}{19{時間}} \approx 4.89{万回/時間} $$

Stray KidsのMV動画の変化の割合

$$ \frac{60 {万回}}{19 {時間}} \approx 3.16 {万回/時間} $$