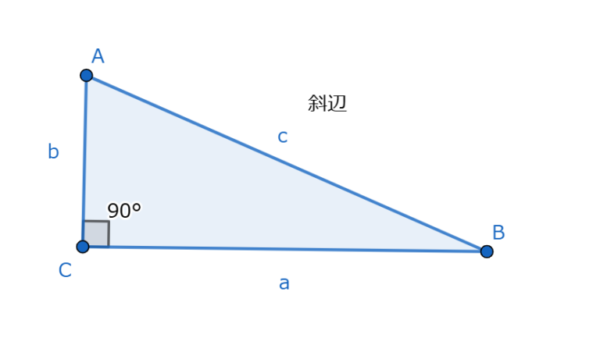
今回は三平方の定理を使って問題を解くときに覚えておくと便利なことを5つ紹介します。テスト対策や確認にご利用ください。
1. 3:4:5の直角三角形
辺の比が3:4:5となっている三角形は直角三角形です。
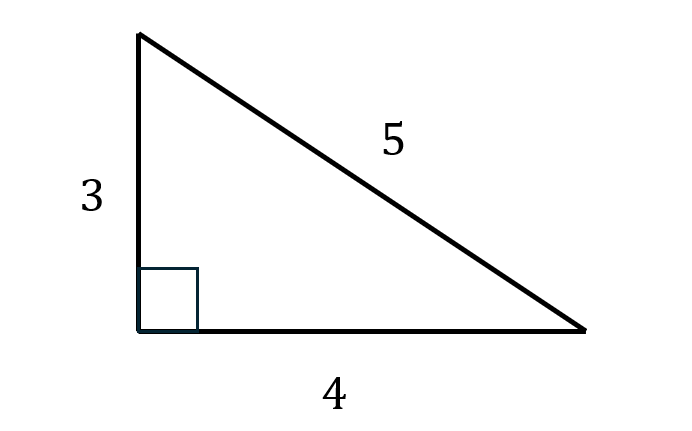
辺の比だけが分かっていて直角三角形であることをこちらが明らかにすることもありますし、

直角三角形であることと2辺が分かっていて残りの辺を求めることもあります。

覚えていると計算や証明の手間が省けます。
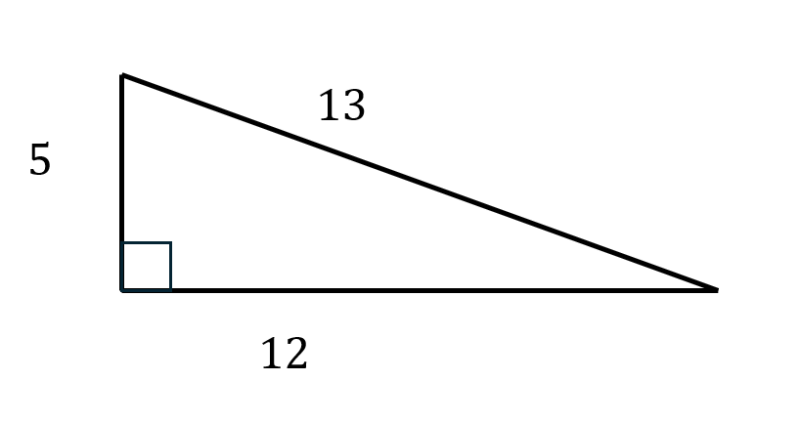
2. 12:13:5の直角三角形
こちらも3:4:5の直角三角形と同様によく出る辺の比の直角三角形です。使い方も3:4:5の直角三角形と同様に使います。
3. \( 1:2:\sqrt{3} \)の直角三角形(角度も決まる)
こちらは辺の比が決まっているだけでなく3つの角度が決まっている直角三角形です。
下の図のように辺の比が\( 1:2:\sqrt{3} \)の三角形は直角三角形です。しかも、その他の角度は30°と60°になります。

角度から辺の比を求める。
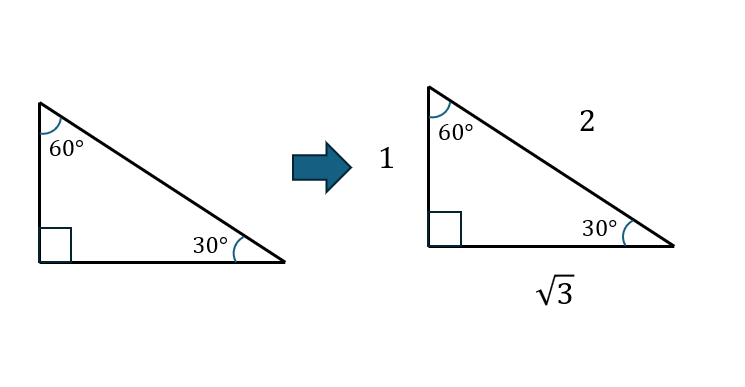
辺の比から角度を求める

角度や辺の比から他の辺の長さを求める。

使い方は多岐にわたります
4. \( 1:1:\sqrt{2} \)の直角三角形(直角二等辺三角形)
先程の\( 1:2:\sqrt{3} \)の直角三角形と同様に、\( 1:1:\sqrt{2} \)の三角形も直角三角形です。
しかも、こちらの場合は直角二等辺三角形になります。
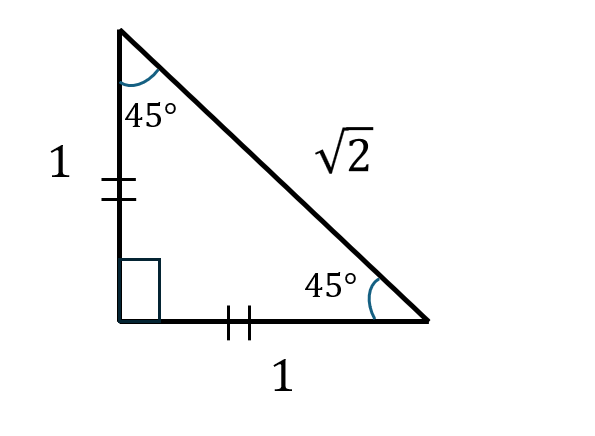
こちらの直角三角形の角度は45°です
このケースも\( 1:2:\sqrt{3} \)の直角三角形と同様に多くの使い方があります
5. 因数分解と三平方の定理
最後に、ちょっとした計算のコツを紹介します。
三平方の定理を使った計算では斜辺を求めることが多いですが、それと同じくらい斜辺以外の長さを求めることも多いです。むしろ斜辺以外を求めることの方が多い?
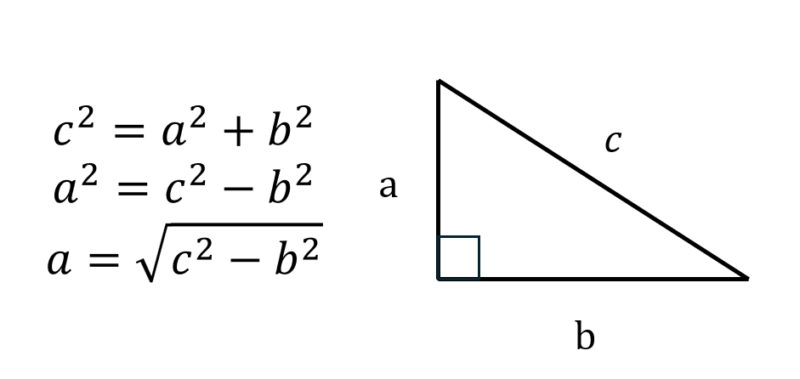
図のように\( a^2 \)について解けるように移項してルートをしてaを求めます。bを求めるときも同様ですね。
aやbを求めるときには必ず2乗の差が出てきます。この形、どこかで見たことはありませんか?
そう、この形は因数分解の公式で出てきましたね。
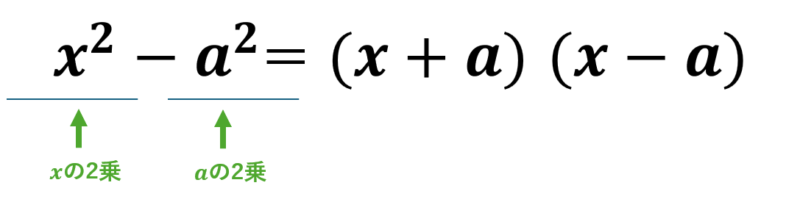
普通に2乗同士を計算しても良いですし、因数分解を使って計算しても良いです。やりやすいほうにしてください。