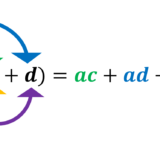文字式は中学で初めて出る考えです。数学では数字だけでなく文字を使って式を作ることが頻発します。この記事では文字式で数式を表すときのルールをまとめます。
テスト勉強や問題演習の時に役立ててください。
- テスト直前で何から手を付けて良いかわからない中学生
- 文字式の計算がちんぷんかんぷんでこのままだと赤点をとってしまうと思っている人
- 中学数学を学びなおしたい大人
- 中学数学を予習したいけど、市販の教材だと難しいと思っている小学生や中学1年生
文字式の積の表し方
[ルール1]文字が含まれるかけ算では、記号 × を省く
- 例: \(x \times y = xy\)
[ルール2]文字式は、アルファベット順に並べることが多い
- 例: \(c \times b \times a = abc\)
[ルール3]数と文字の積では、[数 + 文字] の順に書く
- 例: \(a \times 2 = 2a\)
[ルール4]同じ文字の積は、累乗の指数を用いて表す
- 例: \(a \times a \times a = a^3\)
[ルール5]1 を省く。-1 と文字の積は、− だけを書く
- 例: \(1 \times a = a\)
- 例: \(-1 \times y = -y\)
\(0.1 \times a=0.1a\)です。これは1を省かないので気を付けてください。
文字式の商の表し方
文字式の商を表すときは、÷の記号を使わずに表します。
- 例:\(a \div b=a/b\)
そもそも割り算が分数を使って掛け算にできます。
- 例:\(a \div b=a \times \frac{1}{b}\)
ですので、掛け算の時のルールがそのまま使えます。
文字式の和や差は?
関谷省のルールを見ると和や差はどうなのか気になる人もいるでしょう。
単項式と多項式の次数
この話では以下の数式を使います。
$$ x^2a+4x+5 $$
単項式と多項式とは?
用語解説
単項式:数、文字式の掛け算と割り算で構成されている式
多項式:単項式の和で構成されている式
なんだか難しいですね。もう少しざっくり理解しましょうか。
+や-で区切られた一つ一つが単項式、集めて多項式
今回の式\(x^2a+4x+5\)で見てみると、+や-で区切られた一つ一つを見ると以下のようになります
\(x^2a\)、\(4x\)、\(5\)
これら一つ一つが単項式です。そして、これらを+や-で集めた式\(x^2a+4x+5\)を多項式といいます。
単項式と多項式の違い
人によっては「長ければ多項式、短ければ単項式」といった形で考えてしまうかもしれません。しかし、これはやめてください。おそらく間違えるので。
単項式と多項式の違いは足し算や引き算が式の中にあるかどうか
このポイントで理解してください。
単項式と多項式の違いを理解する例題
例えば下の式は単項式でしょうか?多項式でしょうか?
$$\frac{12345abcdefgxy^2z \alpha}{4566789hijklmnopq \beta}$$
この文字式はめちゃくちゃ長いですね。しかし、単項式です。この式は分解するとこのようになります(長いので横にスクロールしてください)。
$$ \frac{12345abcdefgxy^2z \alpha}{4566789hijklmnopq^4 \beta}=(12345\times a\times b\times c\times d\times e\times f\times g\times x\times y \times y \times z \times \alpha) \div (4566789 \times h \times i \times j\times k\times l\times m\times n\times o\times p\times q\times \beta) $$
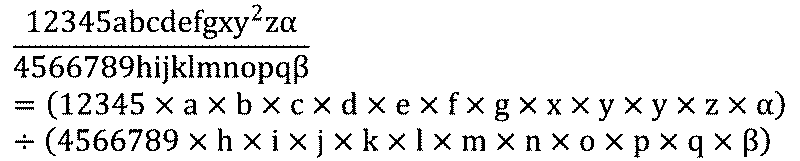
ものすごく長い式ですが、実は掛け算と割り算のみで構成されています。つまり、この式は単項式です。
もうひとつ、これはどうでしょうか?
$$ 1+x $$
こちらは短いですが、足し算が含まれているので多項式です。
項と次数の用語解説
引き続き、多項式\(x^2a+4x+5\)を使って用語の説明します。
項と係数とは?
用語解説
項:多項式の中で、一つ一つの単項式を項といいます
係数:単項式の数の部分を係数といいます。

単項式と多項式の次数とは?
用語解説
・次数:掛け合わされている文字の数。
・単項式の次数:\(a^2\)であれば、\(a \times a\)になり、2つの文字がかけられているので次数は2となります。
・多項式の次数:多項式の場合は項の次数のうちで最も大きいものをその式の次数とみなし、○次式といいます。\(x^2a+4x+5\)であれば、それぞれ次数が3、1、0となり、次数が最も大きい項の次数は3となるので、この多項式は3次式です。

単項式の掛け算と割り算
分解する
単項式の掛け算をするときはまずは分解しましょう。下に、\(3x \times 5y\)の掛け算の方法を示しておきます。
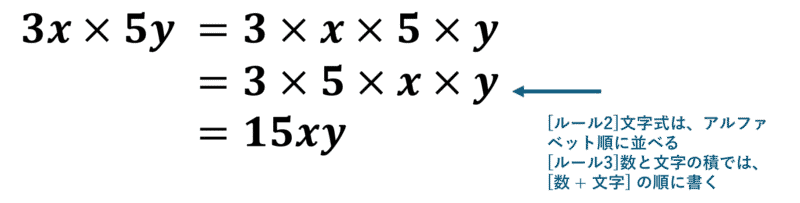
割り算は文字式の位置に注意
単項式の掛け算で一番ミスが多いのはこれなはず。例えば\( \div 2x\)であれば、逆数をかけるので、\( \times \frac{1}{2x}\)になります。計算に慣れていないと\( \div 2x\)を\( \times \frac{x}{2}\)としてしまいますので気を付けてください。
\( \frac{8ab}{3} \div \frac{4a}{9}\)の計算を載せておきます。
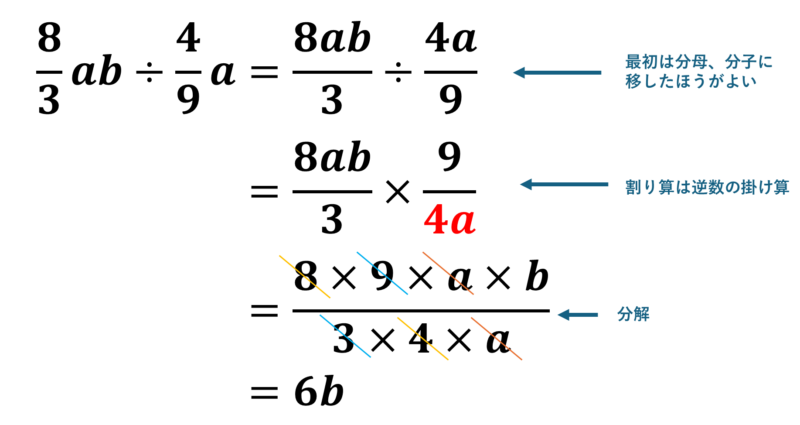
あとは教科書や学校で配布された問題集を使いながら練習してください。
ここまでで単項式の計算は終わりです。
多項式の足し算と引き算
ここからは多項式の計算方法をまとめます。
①同類項をまとめる
②同類項の係数を計算する
実はこれだけです。しかし、この文章だけだと「そもそも同類項がわからない」というコメントもありそうですね。もう少しだけ説明します。
同類項とは?
同類項とは、同じ文字であり同じ次数の項のことです。同じ文字なのはわかりやすいですが、次数も同じでないといけないのがややこしいですね。
①\( a \)と\( 3a \)→これは同じ文字なので同類項です
②\( a \)と\( b \)→これは文字が異なるので同類項ではありません
③\( 3a \)と\( a^2 \)→これは同じ文字ですが次数が異なる(1と2)なので、同類項ではありません
間違えやすいので気を付けてください
同類項をまとめて係数を計算する
同類項はわかりましたか?では実際に計算をしてみましょう。同類項のまとめ方と注意点をまとめておきます
①同じ文字を確認する
②次数を確認
③係数を計算する
下の問題を使ってポイントを実践しましょう。
$$ a + 4a + b -2a$$
この場合\(a , 4a , -2a\)が同類項です。まとめましょう。
$$ a + 4a + b -2a = (a + 4a -2a )+ b $$
次に、まとめた同類項の係数を計算します
$$ (a+4a-2a) = (1+4-2) a =3a $$
同類項でない部分はそれ以上の計算ができないのでこれで終わりです。
$$ a + 4a + b -2a=3a+b$$
多項式同士の足し算と引き算
多項式の足し算は同類項のまとめ方がわかれば多項式の足し算と引き算は簡単です。例題を使って確認しましょう。
$$ (5x+2y)- (3x-3y) $$
先に()を外します。今回、-の後の()を外すときに符号を間違えないように気を付けてください。\( (5x+2y)- (3x-3y)=5x+2y – 3x + 3y \)
この状態で同類項をまとめます。今回でいえば、\( 5x , -3x \)と\( 2y , 3y \)が同類項ですね。\( 5x+2y-3x+3y =5x-3x + 2y+3y \)
ここまで来たら、同類項の係数を計算して終了です。
\begin{array}{l} 5x-3x + 2y+3y &=&(5-3)x +(2+3)y \\ &=& 2x+5y \end{array}
最後に多項式の足し算と引き算のやり方のポイントを載せておきますね。
①同類項をまとめる
②同類項の係数を計算する
多項式の掛け算と割り算
多項式×数、多項式÷数の計算方法
分配法則を使う
$$ a \times (b+c) =ab+ac $$
$$ (b+c) \times a =ab+ac $$
分配法則を使えば簡単に計算できます。例題で確認してみましょう
$$ ①3(2x+5a) $$
これは\( 3(2x+5a)=3 \times (2x+5a) \) ですので、分配法則を使って、
\begin{array}{l} 3 \times (2x+5a) &=& 3 \times 2x +3 \times 5a \\
&=& 6x+15a
\end{array}
と計算できます。
$$ ②(9y-6) \div (-3) $$
割り算も逆数の掛け算なので一緒ですね。
\begin{array}{l} (9y-6) \div (-3) =(9y-6) \times (-\frac{1}{3}) \end{array}
-に気を付けて計算を進めます。
\begin{array}{l} (9y-6) \times (-\frac{1}{3} ) &=& 9y \times (-\frac{1}{3} ) -6 \times (-\frac{1}{3} ) \\
&=& -3y+2 \end{array}
この2問だけで完ぺきとはいかないかもしれませんが、大まかな方針はわかってもらえたと思います。
多項式×多項式は中学3年生で展開公式(乗法公式)として学ぶ!
多項式同士の掛け算は、基本的には分配法則で対処することになります。しかし、計算の機会が多いため、中学3年生で展開公式(乗法公式)として学ぶことになります。
\begin{array}{l} 1.(a+b)(c+d)=ac+ad+bc+bd \\2.(x+a)(x+b)=x^2+(a+b)x+ab \\3.(x+a)^2=x^2+2ax+a^2 \\4.(x-a)^2=x^2-2ax+a^2 \\5.(x+a)(x-a)=x^2-a^2 \\ \end{array}
ちなみに、こちらは右から見ると因数分解の公式になります。こちらの内容は以下の記事に詳しく説明しているのでよかったら読んでください
文字式の代入
式の中の文字に数値を入れることを代入といいます。
文字式というややこしい数式の書き方をしている理由の一つがこの代入です(文字式の代入がどのように役立つのかはまた別の記事で書けたらと思ってます)。
式を整理してから代入をする
計算に慣れていないと、式にそのまま数値を代入したくなると思います。しかし、そのまま入れてはいけません。計算ミスのもとになるからです。まずは式を整理することを忘れないでください。
例題
x=2 ,a=-3の時、以下の式の値を求めなさい
\begin{array}{l}
①3x+ \frac{6}{a} \\
②5(3x+2a)-3(4x+2a)
\end{array}
①はそのまま代入です。
\begin{array}{l}3x+ \frac{6}{a} &=& 3 \times 2 + \frac{6}{-3}\\ &=& 6-2=4 \end{array}
②もそのまま入れたくなると思いますが、ぐっとこらえて式を整理します。
\begin{array}{l} 5(3x+2a)-3(4x+2a) &=& 15x+10a-12x-6a \\
&=& 3x-4a
\end{array}
これでぐっと計算が楽になりましたね。ここに\( x=2 ,a=-3 \)を代入すると、
$$ 3x-4a=3 \times 2 -4 \times (-3) =6+12=18 $$
となり、計算終了です。
ちなみに、\( 5(3x+2a)-3(4x+2a) \)に直接代入すると、
\begin{array}{l} 5(3 \times 2 +2 \times (-3) )-3(4 \times 2+2 \times (-3)) \end{array}
です。どうですか?こちらのほうがミスが増えそうですよね。
「式を整理してから代入をする」の順番を守って、練習してください。
まとめ
今回の記事では中学数学で習う文字式の基本的な知識を一つの記事で一気に復習できるようにしました。
応用問題や練習問題をカットして、可能な限りポイントと公式を簡単に学べるようにしました。問題練習や応用的な話はお持ちの教材を使って行ってください。
この単元は中学数学の中でも面白みがなく、とっつきにくいので人によってはぴんと来ないと思うかもしれません。ですので、この記事を基本知識を確認したらさっさと次の単元や問題演習に移ってください。
正直、この単元をやる意味はここから先を学ばないとピンとこないので
一方で、この単元は一度やり方がわかると機械的に計算すればよいだけなので、テストのときは得点源になります。赤点を取りたくない人はこの単元を練習するのはコスパ、タイパ共に良いでしょう。頑張ってください!