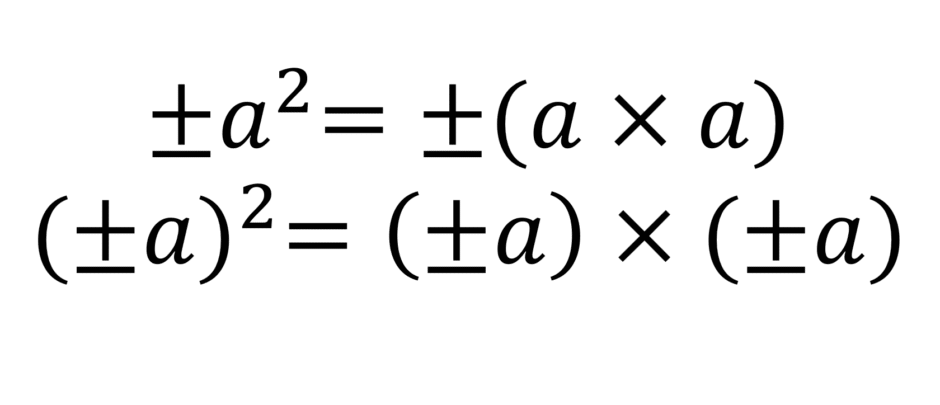今回は中学生で行う計算の中で「累乗の計算」という単元のポイントを簡潔に説明します。難しい話は少ないのですが、ミスしやすいので都度確認してください
ポイント
\(\pm a^2 = \pm (a\times a)\\
(\pm a)^2 = (\pm a)\times (\pm a)\)
覚え方
計算ミスに気を付けてください。
a2の2の部分が「aを何回かけるか」を意味しています。a2であればa×a、a3であればa×a×aとなります。
超簡単な例題
①32
②-32
③(-3)2
解答と解説
①32
解説: 32は 3 × 3 を意味します。
解答: 9
②-32
解説:これが計算ミスをしやすい形の代表です。-32は -(32 )と考えます。つまり、3 を 2 乗してから負の符号をつけます。
解答: -9
③(-3)2
解説:(-3)2 は -3 × -3 を意味します。
解答: 9
少し難しいことを勉強したい君へ
今回は中学数学のメインの2乗を中心に解説しました。しかし、累乗の計算は2乗より大きい累乗でもできます。
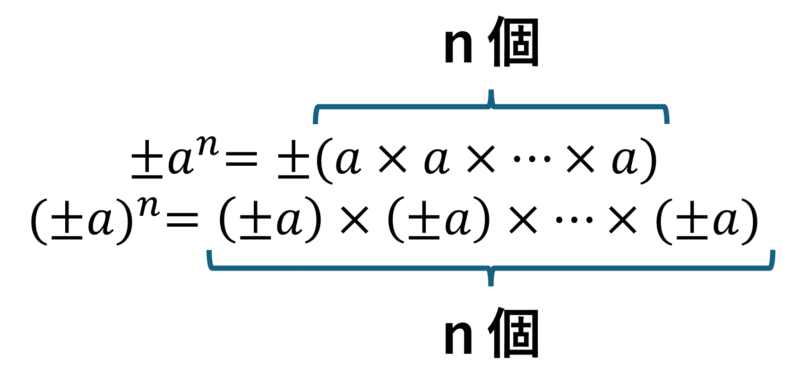
aのn乗とはaをn回かけているということです。nが3でも4でもやろうと思えばいくらでも計算できます
発展例題
\( (-2)^3 \)
\begin{array}{l}
(-2)^3 & =(-2) \times (-2) \times (-2) \\
& = (-1)^3 \times 2^3 \\
& = -8
\end{array}
\( -3^4 \)
\begin{array}{l}
-3^4 & = -(3 \times 3 \times 3 \times 3) \\
& = -81
\end{array}
さらに難しい話
ここまでは中学生の話。ここからは高校生の話です。
実はこちらの図で示したaのn乗。nはいろんな数を入れることができます。具体的には
・負の数
・分数
・小数
等です。こういった数を入れる計算は高校数学の「指数関数」という分野で習います。高校で学ぶその時を楽しみにしていてください(この記事を読んでいるほとんどの人は嫌かもしれませんが)